Relevant publications
Large Scale Data Analysis
Context-aware prompt tuning: advancing in-context learning with adversarial methods

Fine-tuning Large Language Models (LLMs) typically involves updating at least a few billions of parameters. A more parameter-efficient approach is Prompt Tuning (PT), which updates only a few learnable tokens, and differently, In-Context Learning (ICL) adapts the model to a new task by simply including examples in the input without any training. When applying optimization-based methods, such as fine-tuning and PT for few-shot learning, the model is specifically adapted to the small set of training examples, whereas ICL leaves the model unchanged. This distinction makes traditional learning methods more prone to overfitting; in contrast, ICL is less sensitive to the few-shot scenario. While ICL is not prone to overfitting, it does not fully extract the information that exists in the training examples. This work introduces Context-aware Prompt Tuning (CPT), a method inspired by ICL, PT, and adversarial attacks. We build on the ICL strategy of concatenating examples before the input, but we extend this by PT-like learning, refining the context embedding through iterative optimization to extract deeper insights from the training examples. We carefully modify specific context tokens, considering the unique structure of input and output formats. Inspired by adversarial attacks, we adjust the input based on the labels present in the context, focusing on minimizing, rather than maximizing, the loss. Moreover, we apply a projected gradient descent algorithm to keep token embeddings close to their original values, under the assumption that the user-provided data is inherently valuable. Our method has been shown to achieve superior accuracy across multiple classification tasks using various LLM models.
Exploring QUIC dynamics: a large-scale dataset for encrypted traffic analysis

QUIC, a new and increasingly used transport protocol, addresses and resolves the limitations of TCP by offering improved security, performance, and features such as stream multiplexing and connection migration. These features, however, also present challenges for network operators who need to monitor and analyze web traffic. In this paper, we introduce VisQUIC, a labeled dataset comprising over 100,000 QUIC traces from more than 44,000 websites (URLs), collected over a four-month period. These traces provide the foundation for generating more than seven million images, with configurable parameters of window length, pixel resolution, normalization, and labels. These images enable an observer looking at the interactions between a client and a server to analyze and gain insights about QUIC encrypted connections. To illustrate the dataset’s potential, we offer a use-case example of an observer estimating the number of HTTP/3 responses/requests pairs in a given QUIC, which can reveal server behavior, client–server interactions, and the load imposed by an observed connection. We formulate the problem as a discrete regression problem, train a machine learning (ML) model for it, and then evaluate it using the proposed dataset on an example use case.
Scalable unsupervised alignment of general metric and non-metric structures

Aligning data from different domains is a fundamental problem in machine learning with broad applications across very different areas, most notably aligning experimental readouts in single-cell multiomics. Mathematically, this problem can be formulated as the minimization of disagreement of pair-wise quantities such as distances and is related to the Gromov-Hausdorff and Gromov-Wasserstein distances. Computationally, it is a quadratic assignment problem (QAP) that is known to be NP-hard. Prior works attempted to solve the QAP directly with entropic or low-rank regularization on the permutation, which is computationally tractable only for modestly-sized inputs, and encode only limited inductive bias related to the domains being aligned. We consider the alignment of metric structures formulated as a discrete Gromov-Wasserstein problem and instead of solving the QAP directly, we propose to learn a related well-scalable linear assignment problem (LAP) whose solution is also a minimizer of the QAP. We also show a flexible extension of the proposed framework to general non-metric dissimilarities through differentiable ranks. We extensively evaluate our approach on synthetic and real datasets from single-cell multiomics and neural latent spaces, achieving state-of-the-art performance while being conceptually and computationally simple.
Data-driven modeling of interrelated dynamical systems
Non-linear dynamical systems describe numerous real-world phenomena, ranging from the weather, to financial markets and disease progression. Individual systems may share substantial common information, for example patients’ anatomy. Lately, deep-learning has emerged as a leading method for data-driven modeling of non-linear dynamical systems. Yet, despite recent breakthroughs, prior works largely ignored the existence of shared information between different systems. However, such cases are quite common, for example, in medicine: we may wish to have a patient-specific model for some disease, but the data collected from a single patient is usually too small to train a deep-learning model. Hence, we must properly utilize data gathered from other patients. Here, we explicitly consider such cases by jointly modeling multiple systems. We show that the current single-system models consistently fail when trying to learn simultaneously from multiple systems. We suggest a framework for jointly approximating the Koopman operators of multiple systems, while intrinsically exploiting common information. We demonstrate how we can adapt to a new system using order-of-magnitude less new data and show the superiority of our model over competing methods, in terms of both forecasting ability and statistical fidelity, across chaotic, cardiac, and climate systems.
Vector quantile regression on manifolds

Quantile regression (QR) is a statistical tool for distribution-free estimation of conditional quantiles of a target variable given explanatory features. QR is limited by the assumption that the target distribution is univariate and defined on an Euclidean domain. Although the notion of quantiles was recently extended to multi-variate distributions, QR for multi-variate distributions on manifolds remains underexplored, even though many important applications inherently involve data distributed on, e.g., spheres (climate and geological phenomena), and tori (dihedral angles in proteins). By leveraging optimal transport theory and c-concave functions, we meaningfully define conditional vector quantile functions of high-dimensional variables on manifolds (M-CVQFs). Our approach allows for quantile estimation, regression, and computation of conditional confidence sets and likelihoods. We demonstrate the approach’s efficacy and provide insights regarding the meaning of non-Euclidean quantiles through synthetic and real data experiments.
Demystifying graph sparsification algorithms in graph properties preservation

Graph sparsification is a technique that approximates a given graph by a sparse graph with a subset of vertices and/or edges. The goal of an effective sparsification algorithm is to maintain specific graph properties relevant to the downstream task while minimizing the graph’s size. Graph algorithms often suffer from long execution time due to the irregularity and the large real-world graph size. Graph sparsification can be applied to greatly reduce the run time of graph algorithms by substituting the full graph with a much smaller sparsified graph, without significantly degrading the output quality. However, the interaction between numerous sparsifiers and graph properties is not widely explored, and the potential of graph sparsification is not fully understood.
In this work, we cover 16 widely-used graph metrics, 12 representative graph sparsification algorithms, and 14 real-world input graphs spanning various categories, exhibiting diverse characteristics, sizes, and densities. We developed a framework to extensively assess the performance of these sparsification algorithms against graph metrics, and provide insights to the results. Our study shows that there is no one sparsifier that performs the best in preserving all graph properties, e.g. sparsifiers that preserve distance-related graph properties (eccentricity) struggle to perform well on Graph Neural Networks (GNN). This paper presents a comprehensive experimental study evaluating the performance of sparsification algorithms in preserving essential graph metrics. The insights inform future research in incorporating matching graph sparsification to graph algorithms to maximize benefits while minimizing quality degradation. Furthermore, we provide a framework to facilitate the future evaluation of evolving sparsification algorithms, graph metrics, and ever-growing graph data.
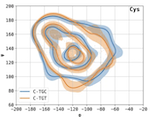
An amino-domino model described by a cross-peptide-bond Ramachandran plot defines amino acid pairs as local structural units
Protein structure, both at the global and local level, dictates function. Proteins fold from chains of amino acids, forming secondary structures, α-helices and β-strands, that, at least for globular proteins, subsequently fold into a three-dimensional structure. Here, we show that a Ramachandran-type plot focusing on the two dihedral angles separated by the peptide bond, and entirely contained within an amino acid pair, defines a local structural unit. We further demonstrate the usefulness of this cross-peptide-bond Ramachandran plot by showing that it captures β-turn conformations in coil regions, that traditional Ramachandran plot outliers fall into occupied regions of our plot, and that thermophilic proteins prefer specific amino acid pair conformations. Further, we demonstrate experimentally that the effect of a point mutation on backbone conformation and protein stability depends on the amino acid pair context, i.e., the identity of the adjacent amino acid, in a manner predictable by our method.
Continuous vector quantile regression

Vector quantile regression (VQR) estimates the conditional vector quantile function (CVQF), a fundamental quantity which fully represents the conditional distribution of Y|X. VQR is formulated as an optimal transport (OT) problem between a uniform U~μ and the target (X,Y)~ν, the solution of which is a unique transport map, co-monotonic with U. Recently NL-VQR has been proposed to estimate support non-linear CVQFs, together with fast solvers which enabled the use of this tool in practical applications. Despite its utility, the scalability and estimation quality of NL-VQR is limited due to a discretization of the OT problem onto a grid of quantile levels. We propose a novel continuous formulation and parametrization of VQR using partial input-convex neural networks (PICNNs). Our approach allows for accurate, scalable, differentiable and invertible estimation of non-linear CVQFs. We further demonstrate, theoretically and experimentally, how continuous CVQFs can be used for general statistical inference tasks: estimation of likelihoods, CDFs, confidence sets, coverage, sampling, and more. This work is an important step towards unlocking the full potential of VQR.
Vector quantile regression on manifolds

Quantile regression (QR) is a statistical tool for distribution-free
estimation of conditional quantiles of a target variable given explanatory
features. QR is limited by the assumption that the target distribution is
univariate and defined on an Euclidean domain. Although the notion of quantiles
was recently extended to multi-variate distributions, QR for multi-variate
distributions on manifolds remains underexplored, even though many important
applications inherently involve data distributed on, e.g., spheres (climate
measurements), tori (dihedral angles in proteins), or Lie groups (attitude in
navigation). By leveraging optimal transport theory and the notion of
c-concave functions, we meaningfully define conditional vector quantile
functions of high-dimensional variables on manifolds (M-CVQFs). Our approach
allows for quantile estimation, regression, and computation of conditional
confidence sets. We demonstrate the approach’s efficacy and provide insights
regarding the meaning of non-Euclidean quantiles through preliminary synthetic
data experiments.
Interpretable deep learning unveils structure-property relationships in polybenzenoid hydrocarbons
In this work, interpretable deep learning was used to identify structure-property relationships governing the HOMO-LUMO gap and relative stability of polybenzenoid hydrocarbons (PBHs). To this end, a ring-based graph representation was used. In addition to affording reduced training times and excellent predictive ability, this representation could be combined with a subunit-based perception of PBHs, allowing chemical insights to be presented in terms of intuitive and simple structural motifs. The resulting insights agree with conventional organic chemistry knowledge and electronic structure-based analyses, and also reveal new behaviors and identify influential structural motifs. In particular, we evaluated and compared the effects of linear, angular, and branching motifs on these two molecular properties, as well as explored the role of dispersion in mitigating torsional strain inherent in non-planar PBHs. Hence, the observed regularities and the proposed analysis contribute to a deeper understanding of the behavior of PBHs and form the foundation for design strategies for new functional PBHs.
Fast nonlinear vector quantile regression

Quantile regression (QR) is a powerful tool for estimating one or more conditional quantiles of a target variable Y given explanatory features X. A limitation of QR is that it is only defined for scalar target variables, due to the formulation of its objective function, and since the notion of quantiles has no standard definition for multivariate distributions. Recently, vector quantile regression (VQR) was proposed as an extension of QR for high-dimensional target variables, thanks to a meaningful generalization of the notion of quantiles to multivariate distributions. Despite its elegance, VQR is arguably not applicable in practice due to several limitations: (i) it assumes a linear model for the quantiles of the target Y given the features X; (ii) its exact formulation is intractable even for modestly-sized problems in terms of target dimensions, the number of regressed quantile levels, or the number of features, and its relaxed dual formulation may violate the monotonicity of the estimated quantiles; (iii) no fast or scalable solvers for VQR currently exist. In this work we fully address these limitations, namely: (i) We extend VQR to the non-linear case, showing substantial improvement over linear VQR; (ii) We propose vector monotone rearrangement, a method which ensures the estimates obtained by VQR relaxations are monotone functions; (iii) We provide fast, GPU-accelerated solvers for linear and nonlinear VQR which maintain a fixed memory footprint with the number of samples and quantile levels, and demonstrate that they scale to millions of samples and thousands of quantile levels; (iv) We release an optimized python package of our solvers as to widespread the use of VQR in real-world applications.
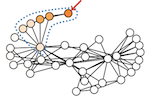
Spectral subgraph localization

Several graph analysis problems are based on some variant of subgraph isomorphism: Given two graphs, G and Q, does G contain a subgraph isomorphic to Q? As this problem is NP-complete, past work usually avoids addressing it explicitly. In this paper, we propose a method that localizes, i.e., finds the best-match position of, Q in G, by aligning their Laplacian spectra and enhance its stability via bagging strategies; we relegate the finding of an exact node correspondence from Q to G to a subsequent and separate graph alignment task. We demonstrate that our localization strategy outperforms a baseline based on the state-of-the-art method for graph alignment in terms of accuracy on real graphs and scales to hundreds of nodes as no other method does.
GRASP: Graph Alignment through Spectral Signatures

What is the best way to match the nodes of two graphs? This graph alignment problem generalizes graph isomorphism and arises in applications from social network analysis to bioinformatics. Some solutions assume that auxiliary information on known matches or node or edge attributes is available, or utilize arbitrary graph features. Such methods fare poorly in the pure form of the problem, in which only graph structures are given. Other proposals translate the problem to one of aligning node embeddings, yet, by doing so, provide only a single-scale view of the graph. In this paper, we transfer the shape-analysis concept of functional maps from the continuous to the discrete case, and treat the graph alignment problem as a special case of the problem of finding a mapping between functions on graphs. We present GRASP, a method that first establishes a correspondence between functions derived from Laplacian matrix eigenvectors, which capture multiscale structural characteristics, and then exploits this correspondence to align nodes. Our experimental study, featuring noise levels higher than anything used in previous studies, shows that GRASP outperforms state-of-the-art methods for graph alignment across noise levels and graph types.
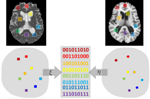
Deep fused two-step cross-modal hashing with multiple semantic supervision

Existing cross-modal hashing methods ignore the informative multimodal joint information and cannot fully exploit the semantic labels. In this paper, we propose a deep fused two-step cross-modal hashing (DFTH) framework with multiple semantic supervision. In the first step, DFTH learns unified hash codes for instances by a fusion network. Semantic label and similarity reconstruction have been introduced to acquire binary codes that are informative, discriminative and semantic similarity preserving. In the second step, two modality-specific hash networks are learned under the supervision of common hash codes reconstruction, label reconstruction, and intra-modal and inter-modal semantic similarity reconstruction. The modality-specific hash networks can generate semantic preserving binary codes for out-of-sample queries. To deal with the vanishing gradients of binarization, continuous differentiable tanh is introduced to approximate the discrete sign function, making the networks able to back-propagate by automatic gradient computation. Extensive experiments on MIRFlickr25K and NUS-WIDE show the superiority of DFTH over state-of-the-art methods.
Intra-class low-rank regularization for supervised and semi-supervised cross-modal retrieval

Cross-modal retrieval aims to retrieve related items across different modalities, for example, using an image query to retrieve related text. The existing deep methods ignore both the intra-modal and inter-modal intra-class low-rank structures when fusing various modalities, which decreases the retrieval performance. In this paper, two deep models (denoted as ILCMR and Semi-ILCMR) based on intra-class low-rank regularization are proposed for supervised and semi-supervised cross-modal retrieval, respectively. Specifically, ILCMR integrates the image network and text network into a unified framework to learn a common feature space by imposing three regularization terms to fuse the cross-modal data. First, to align them in the label space, we utilize semantic consistency regularization to convert the data representations to probability distributions over the classes. Second, we introduce an intra-modal low-rank regularization, which encourages the intra-class samples that originate from the same space to be more relevant in the common feature space. Third, an inter-modal low-rank regularization is applied to reduce the cross-modal discrepancy. To enable the low-rank regularization to be optimized using automatic gradients during network back-propagation, we propose the rank-r approximation and specify the explicit gradients for theoretical completeness. In addition to the three regularization terms that rely on label information incorporated by ILCMR, we propose Semi-ILCMR in the semi-supervised regime, which introduces a low-rank constraint before projecting the general representations into the common feature space. Extensive experiments on four public cross-modal datasets demonstrate the superiority of ILCMR and Semi-ILCMR over other state-of-the-art methods.
Machine learning approaches demonstrate that protein structures carry information about their genetic coding

Synonymous codons translate into the same amino acid. Although the identity of synonymous codons is often considered
inconsequential to the final protein structure there is mounting evidence for an association between the two. Our study
examined this association using regression and classification models, finding that codon sequences predict protein backbone dihedral angles with a lower error than amino acid sequences, and that models trained with true dihedral angles have better classification of synonymous codons given structural information than models trained with random dihedral angles. Using this classification approach, we investigated local codon-codon dependencies and tested whether synonymous codon identity can be predicted more accurately from codon context than amino acid context alone, and most specifically which codon context position carries the most predictive power.
Defining amino acid pairs as structural units suggests mutation sensitivity to adjacent residues

Proteins fold from chains of amino acids, forming secondary structures, α-helices and β-strands, that, at least for globular proteins, subsequently fold into a three-dimensional structure. A large-scale analysis of high-resolution protein structures suggests that amino acid pairs constitute another layer of ordered structure, more local than these conventionally defined secondary structures. We develop a cross-peptide-bond Ramachandran plot that captures the 15 conformational preferences of the amino acid pairs and show that the effect of a particular mutation on the stability of a protein depends in a predictable manner on the adjacent amino acid context.
Codon-specific Ramachandran plots show amino acid backbone conformation depends on identity of the translated codon
Synonymous codons translate into chemically identical amino acids. Once considered inconsequential to the formation of the protein product, there is now significant evidence to suggest that codon usage affects co-translational protein folding and the final structure of the expressed protein. Here we develop a method for computing and comparing codon-specific Ramachandran plots and demonstrate that the backbone dihedral angle distributions of some synonymous codons are distinguishable with statistical significance for some secondary structures. This shows that there exists a dependence between codon identity and backbone torsion of the translated amino acid. Although these findings cannot pinpoint the causal direction of this dependence, we discuss the vast biological implications should coding be shown to directly shape protein conformation and demonstrate the usefulness of this method as a tool for probing associations between codon usage and protein structure. Finally, we urge for the inclusion of exact genetic information into structural databases.
Contrast to divide: Self-supervised pre-training for learning with noisy labels
The success of learning with noisy labels (LNL) methods relies heavily on the success of a warm-up stage where standard supervised training is performed using the full (noisy) training set. In this paper, we identify a” warm-up obstacle”: the inability of standard warm-up stages to train high quality feature extractors and avert memorization of noisy labels. We propose” Contrast to Divide”(C2D), a simple framework that solves this problem by pre-training the feature extractor in a self-supervised fashion. Using self-supervised pre-training boosts the performance of existing LNL approaches by drastically reducing the warm-up stage’s susceptibility to noise level, shortening its duration, and improving extracted feature quality. C2D works out of the box with existing methods and demonstrates markedly improved performance, especially in the high noise regime, where we get a boost of more than 27% for CIFAR-100 with 90% noise over the previous state of the art. In real-life noise settings, C2D trained on mini-WebVision outperforms previous works both in WebVision and ImageNet validation sets by 3% top-1 accuracy. We perform an in-depth analysis of the framework, including investigating the performance of different pre-training approaches and estimating the effective upper bound of the LNL performance with semi-supervised learning.
MetAdapt: Meta-learned task-adaptive architecture for few-shot classification

Few-Shot Learning (FSL) is a topic of rapidly growing interest. Typically, in FSL a model is trained on a dataset consisting of many small tasks (meta-tasks) and learns to adapt to novel tasks that it will encounter during test time. This is also referred to as meta-learning. Another topic closely related to meta-learning with a lot of interest in the community is Neural Architecture Search (NAS), automatically finding optimal architecture instead of engineering it manually. In this work we combine these two aspects of meta-learning. So far, meta-learning FSL methods have focused on optimizing parameters of pre-defined network architectures, in order to make them easily adaptable to novel tasks. Moreover, it was observed that, in general, larger architectures perform better than smaller ones up to a certain saturation point (where they start to degrade due to over-fitting). However, little attention has been given to explicitly optimizing the architectures for FSL, nor to an adaptation of the architecture at test time to particular novel tasks. In this work, we propose to employ tools inspired by the Differentiable Neural Architecture Search (D-NAS) literature in order to optimize the architecture for FSL without over-fitting. Additionally, to make the architecture task adaptive, we propose the concept of ‘MetAdapt Controller’ modules. These modules are added to the model and are meta-trained to predict the optimal network connections for a given novel task. Using the proposed approach we observe state-of-the-art resu
Noise estimation using density estimation for self-supervised multimodal learning

One of the key factors of enabling machine learning models to comprehend and solve real-world tasks is to leverage multimodal data. Unfortunately, the annotation of multimodal data is challenging and expensive. Recently, self-supervised multimodal methods that combine vision and language were proposed to learn multimodal representations without annotation. However, these methods choose to ignore the presence of high levels of noise and thus yield sub-optimal results. In this work, we show that the problem of noise estimation for multimodal data can be reduced to a multimodal density estimation task. Using multimodal density estimation, we propose a noise estimation building block for multimodal representation learning that is based strictly on the inherent correlation between different modalities. We demonstrate how our noise estimation can be broadly integrated and achieves comparable results to state-of-the-art performance on five different benchmark datasets for two challenging multimodal tasks: Video Question Answering and Text-To-Video Retrieval.
Spectral geometric matrix completion

Deep Matrix Factorization (DMF) is an emerging approach to the problem of reconstructing a matrix from a subset of its entries. Recent works have established that gradient descent applied to a DMF model induces an implicit regularization on the rank of the recovered matrix. Despite these promising theoretical results, empirical evaluation of vanilla DMF on real benchmarks exhibits poor reconstructions which we attribute to the extremely low number of samples available. We propose an explicit spectral regularization scheme that is able to make DMF models competitive on real benchmarks, while still maintaining the implicit regularization induced by gradient descent, thus enjoying the best of both worlds.
Single-node attack for fooling graph neural networks
Graph neural networks (GNNs) have shown broad applicability in a variety of domains. Some of these domains, such as social networks and product recommendations, are fertile ground for malicious users and behavior. In this paper, we show that GNNs are vulnerable to the extremely limited scenario of a single-node adversarial example, where the node cannot be picked by the attacker. That is, an attacker can force the GNN to classify any target node to a chosen label by only slightly perturbing another single arbitrary node in the graph, even when not being able to pick that specific attacker node. When the adversary is allowed to pick a specific attacker node, the attack is even more effective. We show that this attack is effective across various GNN types, such as GraphSAGE, GCN, GAT, and GIN, across a variety of real-world datasets, and as a targeted and a non-targeted attack.
Self-Supervised Object Detection and Retrieval Using Unlabeled Videos

Unlabeled video in the wild presents a valuable, yet so far unharnessed, source of information for learning vision tasks. We present the first attempt of fully self-supervised learning of object detection from subtitled videos without any manual object annotation. To this end, we use the How2 multi-modal collection of instructional videos with English subtitles. We pose the problem as learning with a weakly- and noisily-labeled data, and propose a novel training model that can confront high noise levels, and yet train a classifier to localize the object of interest in the video frames, without any manual labeling involved. We evaluate our approach on a set of 11 manually annotated objects in over 5000 frames and compare it to an existing weakly-supervised approach as baseline. Benchmark data and code will be released upon acceptance of the paper.
Intrinsic multi-scale evaluation of generative models

Generative models are often used to sample high-dimensional data points from a manifold with small intrinsic dimension. Existing techniques for comparing generative models focus on global data properties such as mean and covariance; in that sense, they are extrinsic and uni-scale. We develop the first, to our knowledge, intrinsic and multi-scale method for characterizing and comparing underlying data manifolds, based on comparing all data moments by lower-bounding the spectral notion of the Gromov-Wasserstein distance between manifolds. In a thorough experimental study, we demonstrate that our method effectively evaluates the quality of generative models; further, we showcase its efficacy in discerning the disentanglement process in neural networks.
Deep matrix factorization with spectral geometric regularization
We address the problem of reconstructing a matrix from a subset of its entries. Current methods, branded as geometric matrix completion, augment classical rank regularization techniques by incorporating geometric information into the solution. This information is usually provided as graphs encoding relations between rows/columns. In this work, we propose a simple spectral approach for solving the matrix completion problem, via the framework of functional maps. We introduce the zoomout loss, a multiresolution spectral geometric loss inspired by recent advances in shape correspondence, whose minimization leads to state-of-the-art results on various recommender systems datasets. Surprisingly, for some datasets, we were able to achieve comparable results even without incorporating geometric information. This puts into question both the quality of such information and current methods’ ability to use it in a meaningful and efficient way.
Code is available either as Google Colab notebook, or via https://github.com/amitboy/SGMC
DIMAL: Deep isometric manifold learning using sparse geodesic sampling

This paper explores a fully unsupervised deep learning approach for computing distance-preserving maps that generate low-dimensional embeddings for a certain class of manifolds. We use the Siamese configuration to train a neural network to solve the problem of least squares multidimensional scaling for generating maps that approximately preserve geodesic distances. By training with only a few landmarks, we show a significantly improved local and nonlocal generalization of the isometric mapping as compared to analogous non-parametric counterparts. Importantly, the combination of a deep-learning framework with a multidimensional scaling objective enables a numerical analysis of network architectures to aid in understanding their representation power. This provides a geometric perspective to the generalizability of deep learning.
Multidimensional scaling

The various multidimensional scaling models can be broadly classified into metric vs. non-metric, and strain (classical scaling) vs. stress (distance scaling) based MDS models. In metric MDS the goal is to maintain the distances in the embedding space as close as possible to the given dissimilarities, while in nonmetric MDS only the order relations between the dissimilarities are important. Strain-based MDS is an algebraic version of the problem that can be solved by eigenvalue decomposition. Stress-based MDS uses a geometric distortion criterion which results in a non-linear and non-convex optimization problem. Each of these models has its own merits and drawbacks, both numerically and application-wise. On top of these basic models, there exist numerous generalizations, including embedding into non-Euclidean domains, working with different stress models, working in different subspaces, and incorporating machine learning approaches to obtain faster, more accurate and more robust embeddings. This chapter reviews these models, with emphasis on their role in computer vision applications.
ForestHash: Semantic hashing with shallow random forests and tiny convolutional networks
Hash codes are efficient data representations for coping with the ever growing amounts of data. In this paper, we introduce a random forest semantic hashing scheme that embeds tiny convolutional neural networks (CNN) into shallow random forests, with near-optimal information-theoretic code aggregation among trees. We start with a simple hashing scheme, where random trees in a forest act as hashing functions by setting `1′ for the visited tree leaf, and `0′ for the rest. We show that traditional random forests fail to generate hashes that preserve the underlying similarity between the trees, rendering the random forests approach to hashing challenging. To address this, we propose to first randomly group arriving classes at each tee split node into two groups, obtaining a significantly simplified two-class classification problem, which can be handled using a light-weight CNN weak learner. Such random class grouping scheme enables code uniqueness by enforcing each class to share its code with different classes in different trees. A non-conventional low-rank loss is further adopted for the CNN weak learners to encourage code consistency by minimizing intra-class variations and maximizing inter-class distance for the two random class groups. Finally, we introduce an information-theoretic approach for aggregating codes of individual trees into a single hash code, producing a near-optimal unique hash for each class. The proposed approach significantly outperforms state-of-the-art hashing methods for image retrieval tasks on large-scale public datasets, while performing at the level of other state-of-the-art image classification techniques while utilizing a more compact and efficient scalable representation. This work proposes a principled and robust procedure to train and deploy in parallel an ensemble of light-weight CNNs, instead of simply going deeper.
NetLSD: Hearing the shape of a graph
Comparison among graphs is ubiquitous in graph analytics. However, it is a hard task in terms of the expressiveness of the employed similarity measure and the efficiency of its computation. Ideally, graph comparison should be invariant to the order of nodes and the sizes of compared graphs, adaptive to the scale of graph patterns, and scalable. Unfortunately, these properties have not been addressed together. Graph comparisons still rely on direct approaches, graph kernels, or representation-based methods, which are all inefficient and impractical for large graph collections. In this paper, we propose the Network Laplacian Spectral Descriptor (NetLSD): the first, to our knowledge, permutation- and size-invariant, scale-adaptive, and efficiently computable graph representation method that allows for straightforward comparisons of large graphs. NetLSD extracts a compact signature that inherits the formal properties of the Laplacian spectrum, specifically its heat or wave kernel; thus, it hears the shape of a graph. Our evaluation on a variety of real-world graphs demonstrates that it outperforms previous works in both expressiveness and efficiency.
SGR: Self-supervised spectral graph representation learning
Representing a graph as a vector is a challenging task; ideally, the representation should be easily computable and conducive to efficient comparisons among graphs, tailored to the particular data and an analytical task at hand. Unfortunately, a “one-size-fits-all” solution is unattainable, as different analytical tasks may require different attention to global or local graph features. We develop SGR, the first, to our knowledge, method for learning graph representations in a self-supervised manner. Grounded on spectral graph analysis, SGR seamlessly combines all aforementioned desirable properties. In extensive experiments, we show how our approach works on large graph collections, facilitates self-supervised representation learning across a variety of application domains, and performs competitively to state-of-the-art methods without re-training.
Subspace least squares multidimensional scaling
Multidimensional Scaling (MDS) is one of the most popular methods for dimensionality reduction and visualization of high dimensional data. Apart from these tasks, it also found applications in the field of geometry processing for the analysis and reconstruction of non-rigid shapes. In this regard, MDS can be thought of as a shape from metric algorithm, consisting of finding a configuration of points in the Euclidean space that realize, as isometrically as possible, some given distance structure. In the present work we cast the least squares variant of MDS (LS-MDS) in the spectral domain. This uncovers a multiresolution property of distance scaling which speeds up the optimization by a significant amount, while producing comparable, and sometimes even better, embeddings.
Multimodal manifold analysis using simultaneous diagonalization of Laplacians
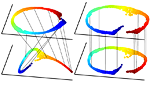
We construct an extension of spectral and diffusion geometry to multiple modalities through simultaneous diagonalization of Laplacian matrices. This naturally extends classical data analysis tools based on spectral geometry, such as diffusion maps and spectral clustering. We provide several synthetic and real examples of manifold learning, retrieval, and clustering demonstrating that the joint spectral geometry frequently better captures the inherent structure of multi-modal data. We also show the relation of many previous approaches to multimodal manifold analysis to our framework, of which the can be seen as particular cases.
Random forests can hash

Hash codes are a very efficient data representation needed to be able to cope with the ever growing amounts of data. We introduce a random forest semantic hashing scheme with information-theoretic code aggregation, showing for the first time how random forest, a technique that together with deep learning have shown spectacular results in classification, can also be extended to large-scale retrieval. Traditional random forest fails to enforce the consistency of hashes generated from each tree for the same class data, i.e., to preserve the underlying similarity, and it also lacks a principled way for code aggregation across trees. We start with a simple hashing scheme, where independently trained random trees in a forest are acting as hashing functions. We the propose a subspace model as the splitting function, and show that it enforces the hash consistency in a tree for data from the same class. We also introduce an information-theoretic approach for aggregating codes of individual trees into a single hash code, producing a near-optimal unique hash for each class. Experiments on large-scale public datasets are presented, showing that the proposed approach significantly outperforms state-of-the-art hashing methods for retrieval tasks.
Multimodal similarity-preserving hashing

We introduce an efficient computational framework for hashing data belonging to multiple modalities into a single representation space where they become mutually comparable. The proposed approach is based on a novel coupled siamese neural network architecture and allows unified treatment of intra- and inter-modality similarity learning. Unlike existing cross-modality similarity learning approaches, our hashing functions are not limited to binarized linear projections and can assume arbitrarily complex forms. We show experimentally that our method significantly outperforms state-of-the-art hashing approaches on multimedia retrieval tasks.
Sparse similarity-preserving hashing

In recent years, a lot of attention has been devoted to efficient nearest neighbor search by means of similarity-preserving hashing. One of the plights of existing hashing techniques is the intrinsic trade-off between performance and computational complexity: while longer hash codes allow for lower false positive rates, it is very difficult to increase the embedding dimensionality without incurring in very high false negatives rates or prohibiting computational costs. In this paper, we propose a way to overcome this limitation by enforcing the hash codes to be sparse. Sparse high-dimensional codes enjoy from the low false positive rates typical of long hashes, while keeping the false negative rates similar to those of a shorter dense hashing scheme with equal number of degrees of freedom. We use a tailored feed-forward neural network for the hashing function. Extensive experimental evaluation involving visual and multi-modal data shows the benefits of the proposed method.
LDAHash: improved matching with smaller descriptors

SIFT-like local feature descriptors are ubiquitously employed in such computer vision applications as content-based retrieval, video analysis, copy detection, object recognition, photo-tourism, and 3D reconstruction from multiple views. Feature descriptors can be designed to be invariant to certain classes of photometric and geometric transformations, in particular, affine and intensity scale transformations. However, real transformations that an image can undergo can only be approximately modeled in this way, and thus most descriptors are only approximately invariant in practice. Secondly, descriptors are usually high-dimensional (e.g. SIFT is represented as a 128-dimensional vector). In large-scale retrieval and matching problems, this can pose challenges in storing and retrieving descriptor data. We propose mapping the descriptor vectors into the Hamming space, in which the Hamming metric is used to compare the resulting representations. This way, we reduce the size of the descriptors by representing them as short binary strings and learn descriptor invariance from examples. We show extensive experimental validation, demonstrating the advantage of the proposed approach.
Data fusion through cross-modality metric learning using similarity-sensitive hashing
Visual understanding is often based on measuring similarity between observations. Learning similarities specific to a certain perception task from a set of examples has been shown advantageous in various computer vision and pattern recognition problems. In many important applications, the data that one needs to compare come from different representations or modalities, and the similarity between such data operates on objects that may have different and often incommensurable structure and dimensionality. In this paper, we propose a framework for supervised similarity learning based on embedding the input data from two arbitrary spaces into the Hamming space. The mapping is expressed as a binary classification problem with positive and negative examples, and can be efficiently learned using boosting algorithms. The utility and efficiency of such a generic approach is demonstrated on several challenging applications including cross-representation shape retrieval and alignment of multi-modal medical images.
Nonlinear dimensionality reduction by topologically constrained isometric embedding
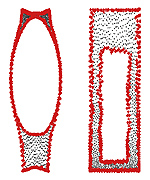
Many manifold learning procedures try to embed a given feature data into a flat space of low dimensionality while preserving as much as possible the metric in the natural feature space. The embedding process usually relies on distances between neighboring features, mainly since distances between features that are far apart from each other often provide an unreliable estimation of the true distance on the feature manifold due to its non-convexity. Distortions resulting from using long geodesics indiscriminately lead to a known limitation of the Isomap algorithm when used to map nonconvex manifolds. Presented is a framework for nonlinear dimensionality reduction that uses both local and global distances in order to learn the intrinsic geometry of flat manifolds with boundaries. The resulting algorithm filters out potentially problematic distances between distant feature points based on the properties of the geodesics connecting those points and their relative distance to the boundary of the feature manifold, thus avoiding an inherent limitation of the Isomap algorithm. Since the proposed algorithm matches non-local structures, it is robust to strong noise. We show experimental results demonstrating the advantages of the proposed approach over conventional dimensionality reduction techniques, both global and local in nature.
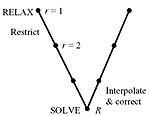
Multigrid multidimensional scaling
Multidimensional scaling (MDS) is a generic name for a family of algorithms that construct a configuration of points in a target metric space from information about inter-point distances measured in some other metric space. Large-scale MDS problems often occur in data analysis, representation, and visualization. Solving such problems efficiently is of key importance in many applications. In this paper, we present a multigrid framework for MDS problems. We demonstrate the performance of our algorithm on dimensionality reduction and isometric embedding problems, two classical problems requiring efficient large-scale MDS. Simulation results show that the proposed approach significantly outperforms conventional MDS algorithms.
A multigrid approach for multi-dimensional scaling
A multigrid approach for the efficient solution of large-scale multidimensional scaling (MDS) problems is presented. The main motivation is a recent application of MDS to isometry-invariant representation of surfaces, in particular, for expression-invariant recognition of human faces. Simulation results show that the proposed approach significantly outperforms conventional MDS algorithms.