Relevant publications
3D Vision & Numerical Geometry
Scalable unsupervised alignment of general metric and non-metric structures

Aligning data from different domains is a fundamental problem in machine learning with broad applications across very different areas, most notably aligning experimental readouts in single-cell multiomics. Mathematically, this problem can be formulated as the minimization of disagreement of pair-wise quantities such as distances and is related to the Gromov-Hausdorff and Gromov-Wasserstein distances. Computationally, it is a quadratic assignment problem (QAP) that is known to be NP-hard. Prior works attempted to solve the QAP directly with entropic or low-rank regularization on the permutation, which is computationally tractable only for modestly-sized inputs, and encode only limited inductive bias related to the domains being aligned. We consider the alignment of metric structures formulated as a discrete Gromov-Wasserstein problem and instead of solving the QAP directly, we propose to learn a related well-scalable linear assignment problem (LAP) whose solution is also a minimizer of the QAP. We also show a flexible extension of the proposed framework to general non-metric dissimilarities through differentiable ranks. We extensively evaluate our approach on synthetic and real datasets from single-cell multiomics and neural latent spaces, achieving state-of-the-art performance while being conceptually and computationally simple.
Deep isometric maps

Isometric feature mapping is an established time-honored algorithm in manifold learning and non-linear dimensionality reduction. Its prominence can be attributed to the output of a coherent global low-dimensional representation of data by preserving intrinsic distances. In order to enable an efficient and more applicable isometric feature mapping, a diverse set of sophisticated advancements have been proposed to the original algorithm to incorporate important factors like sparsity of computation, conformality, topological constraints and spectral geometry. However, a significant shortcoming of most approaches is the dependence on large scale dense-spectral decompositions or the inability to generalize to points far away from the sampling of the manifold.
In this paper, we explore an unsupervised deep learning approach for computing distance-preserving maps for non-linear dimensionality reduction. We demonstrate that our framework is general enough to incorporate all previous advancements and show a significantly improved local and non-local generalization of the isometric mapping. Our approach involves training with only a few landmark datapoints and therefore avoids the need for population of dense matrices as well as computing their spectral decomposition.
Joint optimization of system design and reconstruction in MIMO radar imaging

Multiple-input multiple-output (MIMO) radar is one of the leading depth sensing modalities. However, the usage of multiple receive channels lead to relative high costs and prevent the penetration of MIMOs in many areas such as the automotive industry. Over the last years, few studies concentrated on designing reduced measurement schemes and image reconstruction schemes for MIMO radars, however these problems have been so far addressed separately. On the other hand, recent works in optical computational imaging have demonstrated growing success of simultaneous learningbased design of the acquisition and reconstruction schemes, manifesting significant improvement in the reconstruction quality. Inspired by these successes, in this work, we propose to learn MIMO acquisition parameters in the form of receive (Rx) antenna elements locations jointly with an image neuralnetwork based reconstruction. To this end, we propose an algorithm for training the combined acquisition-reconstruction pipeline end-to-end in a differentiable way. We demonstrate the significance of using our learned acquisition parameters with and without the neural-network reconstruction.
Generating adversarial surfaces via band-limited perturbations
Adversarial attacks have demonstrated remarkable efficacy in altering the output of a learning model by applying a minimal perturbation to the input data. While increasing attention has been placed on the image domain, however, the study of adversarial perturbations for geometric data has been notably lagging behind. In this paper, we show that effective adversarial attacks can be concocted for surfaces embedded in 3D, under weak smoothness assumptions on the perceptibility of the attack. We address the case of deformable 3D shapes in particular, and introduce a general model that is not tailored to any specific surface representation, nor does it assume access to a parametric description of the 3D object.In this context, we consider targeted and untargeted variants of the attack, demonstrating compelling results in either case. We further show how discovering adversarial examples, and then using them for adversarial training, leads to an increase in both robustness and accuracy. Our findings are confirmed empirically over multiple datasets spanning different semantic classes and deformations.
Do we need depth in state-of-the-art face authentication?

Some face recognition methods are designed to utilize geometric features extracted from depth sensors to handle the challenges of single-image based recognition technologies. However, calculating the geometrical data is an expensive and challenging process. Here, we introduce a novel method that learns distinctive geometric features from stereo camera systems without the need to explicitly compute the facial surface or depth map. The raw face stereo images along with coordinate maps allow a CNN to learn geometric features. This way, we keep the simplicity and cost-efficiency of recognition from a single image, while enjoying the benefits of geometric data without explicitly reconstructing it. We demonstrate that the suggested method outperforms both existing single-image and explicit depth-based methods on large-scale benchmarks. We also provide an ablation study to show that the suggested method uses the coordinate maps to encode more informative features.
Hamiltonian operator for spectral shape analysis

Many shape analysis methods treat the geometry of an object as a metric space that can be captured by the Laplace-Beltrami operator. In this paper, we propose to adapt the classical Hamiltonian operator from quantum mechanics to the field of shape analysis. To this end, we study the addition of a potential function to the Laplacian as a generator for dual spaces in which shape processing is performed. We present general optimization approaches for solving variational problems involving the basis defined by the Hamiltonian using perturbation theory for its eigenvectors. The suggested operator is shown to produce better functional spaces to operate with, as demonstrated on different shape analysis tasks.
Self-supervised learning of dense shape correspondence
We introduce the first completely unsupervised correspondence learning approach for deformable 3D shapes. Key to our model is the understanding that natural deformations (such as changes in the pose) approximately preserve the metric structure of the surface, yielding a natural criterion to drive the learning process toward distortion-minimizing predictions. On this basis, we overcome the need for annotated data and replace it with a purely geometric criterion. The resulting learning model is class-agnostic and is able to leverage any type of deformable geometric data for the training phase. In contrast to existing supervised approaches which specialize in the class seen at training time, we demonstrate stronger generalization as well as applicability to a variety of challenging settings. We showcase our method on a wide selection of correspondence benchmarks, where we outperform other methods in terms of accuracy, generalization, and efficiency.
Intel RealSense SR300 Coded light depth Camera

Intel RealSense SR300 is a depth camera capable of providing a VGA-size depth map at 60 fps and 0.125mm depth resolution. In addition, it outputs an infrared VGA-resolution image and a 1080p color texture image at 30 fps.
SR300 form-factor enables it to be integrated into small consumer products and as a front-facing camera in laptops and Ultrabooks. The SR300 depth camera is based on a coded-light technology where triangulation between projected patterns and images captured by a dedicated sensor is used to produce the depth map. Each projected line is coded by a special temporal optical code, that enables a dense depth map reconstruction from its reflection. The solid mechanical assembly of the camera allows it to stay calibrated throughout temperature and pressure changes, drops, and hits. In addition, active dynamic control maintains a calibrated depth output. An extended API LibRS released with the camera allows developers to integrate the camera in various applications. Algorithms for 3D scanning, facial analysis, hand gesture recognition, and tracking are within reach for applications using the SR300. In this paper, we describe the underlying technology, hardware, and algorithms of the SR300, as well as its calibration procedure, and outline some use cases. We believe that this paper will provide a full case study of a mass-produced depth sensing product and technology.
Correspondence-free region localization for partial shape similarity via Hamiltonian spectrum alignment
We consider the problem of localizing relevant subsets of non-rigid geometric shapes given only a partial 3D query as the input. Such problems arise in several challenging tasks in 3D vision and graphics, including partial shape similarity, retrieval, and non-rigid correspondence. We phrase the problem as one of alignment between short sequences of eigenvalues of basic differential operators, which are constructed upon a scalar function defined on the 3D surfaces. Our method therefore seeks for a scalar function that entails this alignment. Differently from existing approaches, we do not require solving for a correspondence between the query and the target, therefore greatly simplifying the optimization process; our core technique is also descriptor-free, as it is driven by the geometry of the two objects as encoded in their operator spectra. We further show that our spectral alignment algorithm provides a remarkably simple alternative to the recent shape-from-spectrum reconstruction approaches. For both applications, we demonstrate improvement over the state-of-the-art either in terms of accuracy or computational cost.
Shape Correspondence with Isometric and Non-Isometric Deformations

The registration of surfaces with non-rigid deformation, especially non-isometric deformations, is a challenging problem. When applying such techniques to real scans, the problem is compounded by topological and geometric inconsistencies between shapes. In this paper, we capture a benchmark dataset of scanned 3D shapes undergoing various controlled deformations (articulating, bending, stretching and topologically changing), along with ground truth correspondences. With the aid of this tiered benchmark of increasingly challenging real scans, we explore this problem and investigate how robust current state-of-the-art methods perform in different challenging registration and correspondence scenarios. We discover that changes in topology is a challenging problem for some methods and that machine learning-based approaches prove to be more capable of handling non-isometric deformations on shapes that are moderately similar to the training set.
DIMAL: Deep isometric manifold learning using sparse geodesic sampling

This paper explores a fully unsupervised deep learning approach for computing distance-preserving maps that generate low-dimensional embeddings for a certain class of manifolds. We use the Siamese configuration to train a neural network to solve the problem of least squares multidimensional scaling for generating maps that approximately preserve geodesic distances. By training with only a few landmarks, we show a significantly improved local and nonlocal generalization of the isometric mapping as compared to analogous non-parametric counterparts. Importantly, the combination of a deep-learning framework with a multidimensional scaling objective enables a numerical analysis of network architectures to aid in understanding their representation power. This provides a geometric perspective to the generalizability of deep learning.
Partial single- and multi-shape dense correspondence using functional maps

Shape correspondence is a fundamental problem in computer graphics and vision, with applications in various problems including animation, texture mapping, robotic vision, medical imaging, archaeology and many more. In settings where the shapes are allowed to undergo non-rigid deformations and only partial views are available, the problem becomes very challenging. In this chapter we describe recent techniques designed to tackle such problems. Specifically, we explain how the renown functional maps framework can be extended to tackle the partial setting. We then present a further extension to the mutli-part case in which one tries to establish correspondence between a collection of shapes. Finally, we focus on improving the technique efficiency, by disposing of its spatial ingredient and thus keeping the computation in the spectral domain. Extensive experimental results are provided along with the theoretical explanations, to demonstrate the effectiveness of the described methods in these challenging scenarios.
Multidimensional scaling

The various multidimensional scaling models can be broadly classified into metric vs. non-metric, and strain (classical scaling) vs. stress (distance scaling) based MDS models. In metric MDS the goal is to maintain the distances in the embedding space as close as possible to the given dissimilarities, while in nonmetric MDS only the order relations between the dissimilarities are important. Strain-based MDS is an algebraic version of the problem that can be solved by eigenvalue decomposition. Stress-based MDS uses a geometric distortion criterion which results in a non-linear and non-convex optimization problem. Each of these models has its own merits and drawbacks, both numerically and application-wise. On top of these basic models, there exist numerous generalizations, including embedding into non-Euclidean domains, working with different stress models, working in different subspaces, and incorporating machine learning approaches to obtain faster, more accurate and more robust embeddings. This chapter reviews these models, with emphasis on their role in computer vision applications.
Functional maps representation on product manifolds

We consider the tasks of representing, analyzing and manipulating maps between shapes. We model maps as densities over the product manifold of the input shapes; these densities can be treated as scalar functions and therefore are manipulable using the language of signal processing on manifolds. Being a manifold itself, the product space endows the set of maps with a geometry of its own, which we exploit to define map operations in the spectral domain; we also derive relationships with other existing representations (soft maps and functional maps). To apply these ideas in practice, we discretize product manifolds and their Laplace-Beltrami operators, and we introduce localized spectral analysis of the product manifold as a novel tool for map processing. Our framework applies to maps defined between and across 2D and 3D shapes without requiring special adjustment, and it can be implemented efficiently with simple operations on sparse matrices.
Deep Functional Maps: Structured prediction for dense shape correspondence
We introduce a new framework for learning dense correspondence between deformable 3D shapes. Existing learning based approaches model shape correspondence as a labelling problem, where each point of a query shape receives a label identifying a point on some reference domain; the correspondence is then constructed a posteriori by composing the label predictions of two input shapes. We propose a paradigm shift and design a structured prediction model in the space of functional maps, linear operators that provide a compact representation of the correspondence. We model the learning process via a deep residual network which takes dense descriptor fields defined on two shapes as input, and outputs a soft map between the two given objects. The resulting correspondence is shown to be accurate on several challenging benchmarks comprising multiple categories, synthetic models, real scans with acquisition artifacts, topological noise, and partiality.
Efficient deformable shape correspondence via kernel matching
We present a method to match three dimensional shapes under non-isometric deformations, topology changes and partiality. We formulate the problem as matching between a set of pair-wise and point-wise descriptors, imposing a continuity prior on the mapping, and propose a projected descent optimization procedure inspired by difference of convex functions (DC) programming. Surprisingly, in spite of the highly non-convex nature of the resulting quadratic assignment problem, our method converges to a semantically meaningful and continuous mapping in most of our experiments, and scales well. We provide preliminary theoretical analysis and several interpretations of the method.
Product Manifold Filter: Non-rigid shape correspondence via kernel density estimation in the product space
Many algorithms for the computation of correspondences between deformable shapes rely on some variant of nearest neighbor matching in a descriptor space. Such are, for example, various point-wise correspondence recovery algorithms used as a post-processing stage in the functional correspondence framework. Such frequently used techniques implicitly make restrictive assumptions (e.g., near-isometry) on the considered shapes and in practice suffer from a lack of accuracy and result in poor surjectivity. We propose an alternative recovery technique capable of guaranteeing a bijective correspondence and producing significantly higher accuracy and smoothness. Unlike other methods, our approach does not depend on the assumption that the analyzed shapes are isometric. We derive the proposed method from the statistical framework of kernel density estimation and demonstrate its performance on several challenging deformable 3D shape matching datasets.
Fully spectral partial shape matching

We propose an efficient procedure for calculating partial dense intrinsic correspondence between deformable shapes performed entirely in the spectral domain. Our technique relies on the recently introduced partial functional maps formalism and on the joint approximate diagonalization (JAD) of the Laplace-Beltrami operators previously introduced for matching non-isometric shapes. We show that a variant of the JAD problem with an appropriately modified coupling term (surprisingly) allows to construct quasi-harmonic bases localized on the latent corresponding parts. This circumvents the need to explicitly compute the unknown parts by means of the cumbersome alternating minimization used in the previous approaches, and allows performing all the calculations in the spectral domain with constant complexity independent of the number of shape vertices. We provide an extensive evaluation of the proposed technique on standard non-rigid correspondence benchmarks and show state-of-the-art performance in various settings, including partiality and the presence of topological noise.
Subspace least squares multidimensional scaling
Multidimensional Scaling (MDS) is one of the most popular methods for dimensionality reduction and visualization of high dimensional data. Apart from these tasks, it also found applications in the field of geometry processing for the analysis and reconstruction of non-rigid shapes. In this regard, MDS can be thought of as a shape from metric algorithm, consisting of finding a configuration of points in the Euclidean space that realize, as isometrically as possible, some given distance structure. In the present work we cast the least squares variant of MDS (LS-MDS) in the spectral domain. This uncovers a multiresolution property of distance scaling which speeds up the optimization by a significant amount, while producing comparable, and sometimes even better, embeddings.
Cloud Dictionary: Sparse coding and modeling for point clouds

With the development of range sensors such as LIDAR and time-of-flight cameras, 3D point cloud scans have become ubiquitous in computer vision applications, the most prominent ones being gesture recognition and autonomous driving. Parsimony-based algorithms have shown great success on images and videos where data points are sampled on a regular Cartesian grid. We propose an adaptation of these techniques to irregularly sampled signals by using continuous dictionaries. We present an example application in the form of point cloud denoising.
ASIST: Automatic Semantically Invariant Scene Transformation

We present ASIST, a technique for transforming point clouds by replacing objects with their semantically equivalent counterparts. Transformations of this kind have applications in virtual reality, repair of fused scans, and robotics. ASIST is based on a unified formulation of semantic labeling and object replacement; both result from minimizing a single objective. We present numerical tools for the efficient solution of this optimization problem. The method is experimentally assessed on new datasets of both synthetic and real point clouds, and is additionally compared to two recent works on object replacement on data from the corresponding papers.
Computing and processing correspondences with functional maps

Notions of similarity and correspondence between geometric shapes and images are central to many tasks in geometry processing, computer vision, and computer graphics. The goal of this course is to familiarize the audience with a set of recent techniques that greatly facilitate the computation of mappings or correspondences between geometric datasets, such as 3D shapes or 2D images by formulating them as mappings between functions rather than points or triangles. Methods based on the functional map framework have recently led to state-of-the-art results in problems as diverse as non-rigid shape matching, image co-segmentation and even some aspects of tangent vector field design. One challenge in adopting these methods in practice, however, is that their exposition often assumes a significant amount of background in geometry processing, spectral methods and functional analysis, which can make it difficult to gain an intuition about their performance or about their applicability to real-life problems. In this course, we try to provide all the tools necessary to appreciate and use these techniques, while assuming very little background knowledge. We also give a unifying treatment of these techniques, which may be difficult to extract from the individual publications and, at the same time, hint at the generality of this point of view, which can help tackle many problems in the analysis and creation of visual content. This course is structured as a half day course. We will assume that the participants have knowledge of basic linear algebra and some knowledge of differential geometry, to the extent of being familiar with the concepts of a manifold and a tangent vector space. We will discuss in detail the functional approach to finding correspondences between non-rigid shapes, the design and analysis of tangent vector fields on surfaces, consistent map estimation in networks of shapes and applications to shape and image segmentation, shape variability analysis, and other areas.
Hamiltonian operator for spectral shape analysis

Many shape analysis methods treat the geometry of an object as a metric space that can be captured by the Laplace-Beltrami operator. In this paper, we propose to adapt the classical Hamiltonian operator from quantum me- chanics to the field of shape analysis. To this end we study the addition of a potential function to the Laplacian as a generator for dual spaces in which shape processing is performed. We present a general optimization approach for solving variational problems involving the basis defined by the Hamilto- nian using perturbation theory for its eigenvectors. The suggested operator is shown to produce better functional spaces to operate with, as demon- strated on different shape analysis tasks.
Consistent discretization and minimization of the L1 norm on manifolds

The L1 norm has been tremendously popular in signal and image processing in the past two decades due to its sparsity-promoting properties. More recently, its generalization to non-Euclidean domains has been found useful in shape analysis applications. For example, in conjunction with the minimization of the Dirichlet energy, it was shown to produce a compactly supported quasi-harmonic orthonormal basis, dubbed as compressed manifold modes. The continuous L1 norm on the manifold is often replaced by the vector l1 norm applied to sampled functions. We show that such an approach is incorrect in the sense that it does not consistently discretize the continuous norm and warn against its sensitivity to the specific sampling. We propose two alternative discretizations resulting in an iteratively-reweighed l2 norm. We demonstrate the proposed strategy on the compressed modes problem, which reduces to a sequence of simple eigendecomposition problems not requiring non-convex optimization on Stiefel manifolds and producing more stable and accurate results.
SpectroMeter: Amortized sublinear spectral approximation of distance on graphs
We present a method to approximate pairwise distance on a graph, having an amortized sub-linear complexity in its size. The proposed method follows the so-called heat method due to Crane et al. The only additional input is the values of the eigenfunctions of the graph Laplacian at a subset of the vertices. Using these values we estimate a random walk from the source points, and normalize the result into a unit gradient function. The eigenfunctions are then used to synthesize distance values abiding by these constraints at desired locations. We show that this method works in practice on different types of inputs ranging from triangular meshes to general graphs. We also demonstrate that the resulting approximate distance is accurate enough to be used as the input to a recent method for intrinsic shape correspondence computation.
Non-rigid puzzles

Shape correspondence is a fundamental problem in computer graphics and vision, with applications in various problems including animation, texture mapping, robotic vision, medical imaging, archaeology and many more. In settings where the shapes are allowed to undergo non-rigid deformations and only partial views are available, the problem becomes very challenging. To this end, we present a non-rigid multi-part shape matching algorithm. We assume to be given a reference shape and its multiple parts undergoing a non-rigid deformation. Each of these query parts can be additionally contaminated by clutter, may overlap with other parts, and there might be missing parts or redundant ones. Our method simultaneously solves for the segmentation of the reference model, and for a dense correspondence to (subsets of) the parts. Experimental results on synthetic as well as real scans demonstrate the effectiveness of our method in dealing with this challenging matching scenario.
Shape retrieval of non-rigid 3D human models
3D models of humans are commonly used within computer graphics and vision, and so the ability to distinguish between body shapes is an important shape retrieval problem. We extend our recent paper which provided a benchmark for testing non-rigid 3D shape retrieval algorithms on 3D human models. This benchmark provided a far stricter challenge than previous shape benchmarks.We have added 145 new models for use as a separate training set, in order to standardise the training data used and provide a fairer comparison. We have also included experiments with the FAUST dataset of human scans. All participants of the previous benchmark study have taken part in the new tests reported here, many providing updated results using the new data. In addition, further participants have also taken part, and we provide extra analysis of the retrieval results. A total of 25 different shape retrieval methods are compared.
SHREC'15 Track: Scalability of non-rigid 3D shape retrieval
Due to recent advances in 3D acquisition and modeling, increasingly large amounts of 3D shape data become available in many application domains. This rises not only the need for effective methods for 3D shape retrieval, but also efficient retrieval and robust implementations. Previous 3D retrieval challenges have mainly considered data sets in the range of a few thousands of queries. In the 2015 SHREC track on Scalability of 3D Shape Retrieval we provide a benchmark with more than 96 thousand shapes. The data set is based on a non-rigid retrieval benchmark enhanced by other existing shape benchmarks. From the baseline models, a large set of partial objects were automatically created by simulating a range-image acquisition process. Four teams have participated in the track, with most methods providing very good to near-perfect retrieval results, and one less complex baseline method providing fair performance. Timing results indicate that three of the methods including the latter baseline one provide near- interactive time query execution. Generally, the cost of data pre-processing varies depending on the method.
Probably approximately symmetric: Fast rigid symmetry detection with global guarantees
We present a fast algorithm for global 3D symmetry detection with approximation guarantees. The algorithm is guaranteed to find the best approximate symmetry of a given shape, to within a user-specified threshold, with very high probability. Our method uses a carefully designed sampling of the transformation space, where each transformation is efficiently evaluated using a sub-linear algorithm. We prove that the density of the sampling depends on the total variation of the shape, allowing us to derive formal bounds on the algorithm’s complexity and approximation quality. We further investigate different volumetric shape representations (in the form of truncated distance transforms), and in such a way control the total variation of the shape and hence the sampling density and the runtime of the algorithm. A comprehensive set of experiments assesses the proposed method, including an evaluation on the eight categories of the COSEG data-set. This is the first large-scale evaluation of any symmetry detection technique that we are aware of.
Supervised learning of bag-of-features shape descriptors using sparse coding

We present a method for supervised learning of shape descriptors for shape retrieval applications. Many content-based shape retrieval approaches follow the bag-of-features (BoF) paradigm commonly used in text and image retrieval by first computing local shape descriptors, and then representing them in a `geometric dictionary’ using vector quantization. A major drawback of such approaches is that the dictionary is constructed in an unsupervised manner using clustering, unaware of the last stage of the process (pooling of the local descriptors into a BoF, and comparison of the latter using some metric). In this paper, we replace the clustering with dictionary learning, where every atom acts as a feature, followed by sparse coding and pooling to get the final BoF descriptor. Both the dictionary and the sparse codes can be learned in the supervised regime via bi-level optimization using a task-specific objective that promotes invariance desired in the specific application. We show significant performance improvement on several standard shape retrieval benchmarks.
Quantifying 3D shape similarity using maps: Recent trends, applications and perspectives
Shape similarity is an acute issue in Computer Vision and Computer Graphics that involves many aspects of human perception of the real world, including judged and perceived similarity concepts, deterministic and probabilistic decisions and their formalization. 3D models carry multiple information with them (e.g., geometry, topology, texture, time evolution, appearance), which can be thought as the filter that drives the recognition process. Assessing and quantifying the similarity between 3D shapes is necessary to explore large dataset of shapes, and tune the analysis framework to the userÕs needs. Many efforts have been done in this sense, including several attempts to formalize suitable notions of similarity and distance among 3D objects and their shapes. In the last years, 3D shape analysis knew a rapidly growing interest in a number of challenging issues, ranging from deformable shape similarity to partial matching and view-point selection. In this panorama, we focus on methods which quantify shape similarity (between two objects and sets of models) and compare these shapes in terms of their properties (i.e., global and local, geometric, differential and topological) conveyed by (sets of) maps. After presenting in detail the theoretical foundations underlying these methods, we review their usage in a number of 3D shape application domains, ranging from matching and retrieval to annotation and segmentation. Particular emphasis will be given to analyze the suitability of the different methods for specific classes of shapes (e.g. rigid or isometric shapes), as well as the flexibility of the various methods at the different stages of the shape comparison process. Finally, the most promising directions for future research developments are discussed.
Equi-affine invariant intrinsic geometries for bendable shapes analysis
Traditional models of bendable surfaces are based on the exact or approximate invariance to deformations that do not tear or stretch the shape, leaving intact an intrinsic geometry associated with it. Intrinsic geometries are typically defined using either the shortest path length (geodesic distance), or properties of heat diffusion (diffusion distance) on the surface. Both ways are implicitly derived from the metric induced by the ambient Euclidean space. In this paper, we depart from this restrictive assumption by observing that a different choice of the metric results in a richer set of geometric invariants. We extend the classic equi-affine arclength, defined on convex surfaces, to arbitrary shapes with non-vanishing gaussian curvature. As a result, a family of affine- invariant intrinsic geometries is obtained. The potential of this novel framework is explored in a wide range of applications such as shape matching and retrieval, symmetry detection, and computation of Voroni tessellation. We show that in some shape analysis tasks, our affine-invariant intrinsic geometries often outperform their Euclidean-based counterparts.
Shape retrieval of non-rigid 3D human models

We have created a new dataset for non-rigid 3D shape retrieval, one that is much more challenging than existing datasets. Our dataset features exclusively human models, in a variety of body shapes and poses. 3D models of humans are commonly used within computer graphics and vision, therefore the ability to distinguish between body shapes is an important feature for shape retrieval methods. In this track nine groups have submitted the results of a total of 22 different methods which have been tested on our new dataset.
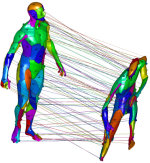
Sparse modeling of intrinsic correspondences
We present a novel sparse modeling approach to non-rigid shape matching using only the ability to detect repeatable regions. As the input to our algorithm, we are given only two sets of regions in two shapes; no descriptors are provided so the correspondence between the regions is not know, nor we know how many regions correspond in the two shapes. We show that even with such scarce information, it is possible to establish very accurate correspondence between the shapes by using methods from the field of sparse modeling, being this, the first non-trivial use of sparse models in shape correspondence. We formulate the problem of permuted sparse coding, in which we solve simultaneously for an unknown permutation ordering the regions on two shapes and for an unknown correspondence in functional representation. We also propose a robust variant capable of handling incomplete matches. Numerically, the problem is solved efficiently by alternating the solution of a linear assignment and a sparse coding problem. The proposed methods are evaluated qualitatively and quantitatively on standard benchmarks containing both synthetic and scanned objects.
Coupled quasi-harmonic bases

State-of-the-art approaches to shape analysis, synthesis, and correspondence rely on these natural harmonic bases that allow using classical tools from harmonic analysis on manifolds. However, many applications involving multiple shapes are obstacled by the fact that Laplacian eigenbases computed independently on different shapes are often incompatible with each other. In this paper, we propose the construction of common approximate eigenbases for multiple shapes using approximate joint diagonalization algorithms, taking as input a set of corresponding functions (e.g. indicator functions of stable regions) on the two shapes. We illustrate the benefits of the proposed approach on tasks from shape editing, pose transfer, correspondence, and similarity.
Geometric and photometric data fusion in non-rigid shape analysis

In this paper, we explore the use of the diffusion geometry framework for the fusion of geometric and photometric information in local and global shape descriptors. Our construction is based on the definition of a diffusion process on the shape manifold embedded into a high-dimensional space where the embedding coordinates represent the photometric information. Experimental results show that such data fusion is useful in coping with different challenges of shape analysis where pure geometric and pure photometric methods fail.
Partial shape matching without point-wise correspondence

Partial similarity of shapes in a challenging problem arising in many important applications in computer vision, shape analysis, and graphics, e.g. when one has to deal with partial information and acquisition artifacts. The problem is especially hard when the underlying shapes are non-rigid and are given up to a deformation. Partial matching is usually approached by computing local descriptors on a pair of shapes and then establishing a point-wise non-bijective correspondence between the two, taking into account possibly different parts. In this paper, we introduce an alternative correspondence-less approach to matching fragments to an entire shape undergoing a non-rigid deformation. We use diffusion geometric descriptors and optimize over the integration domains on which the integral descriptors of the two parts match. The problem is regularized using the Mumford-Shah functional. We show an efficient discretization based on the Ambrosio-Tortorelli approximation generalized to triangular meshes and point clouds, and present experiments demonstrating the success of the proposed method.
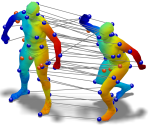
Learning spectral descriptors for deformable shape correspondence
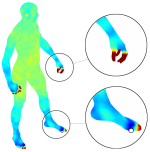
Informative and discriminative feature descriptors play a fundamental role in deformable shape analysis. For example, they have been successfully employed in correspondence, registration, and retrieval tasks. In the recent years, significant attention has been devoted to descriptors obtained from the spectral decomposition of the Laplace-Beltrami operator associated with the shape. Notable examples in this family are the heat kernel signature (HKS) and the recently introduced wave kernel signature (WKS). Laplacian-based descriptors achieve state-of-the-art performance in numerous shape analysis tasks; they are computationally efficient, isometry-invariant by construction, and can gracefully cope with a variety of transformations. In this paper, we formulate a generic family of parametric spectral descriptors. We argue that in order to be optimized for a specific task, the descriptor should take into account the statistics of the corpus of shapes to which it is applied (the “signal”) and those of the class of transformations to which it is made insensitive (the “noise”). While such statistics are hard to model axiomatically, they can be learned from examples. Following the spirit of the Wiener filter in signal processing, we show a learning scheme for the construction of optimized spectral descriptors and relate it to Mahalanobis metric learning. The superiority of the proposed approach in generating correspondences is demonstrated on synthetic and scanned human figures. We also show that the learned descriptors are robust enough to be learned on synthetic data and transferred successfully to scanned shapes.
Putting the pieces together: regularized multi-shape partial matching

Multi-part shape matching in an important class of problems, arising in many fields such as computational archaeology, biology, geometry processing, computer graphics and vision. In this paper, we address the problem of simultaneous matching and segmentation of multiple shapes. We assume to be given a reference shape and multiple parts partially matching the reference. Each of these parts can have additional clutter, have overlap with other parts, or there might be missing parts. We show experimental results of efficient and accurate assembly of fractured synthetic and real objects.
Stable spectral mesh filtering

The rapid development of 3D acquisition technology has brought with itself the need to perform standard signal processing operations such as filters on 3D data. It has been shown that the eigenfunctions of the Laplace-Beltrami operator (manifold harmonics) of a surface play the role of the Fourier basis in the Euclidean space; it is thus possible to formulate signal analysis and synthesis in the manifold harmonics basis. In particular, geometry filtering can be carried out in the manifold harmonics domain by decomposing the embedding coordinates of the shape in this basis. However, since the basis functions depend on the shape itself, such filtering is valid only for weak (near all-pass) filters, and produces severe artifacts otherwise. In this paper, we analyze this problem and propose the fractional filtering approach, wherein we apply iteratively weak fractional powers of the filter, followed by the update of the basis functions. Experimental results show that such a process produces more plausible and meaningful results.
Intrinsic shape context descriptors for deformable shapes
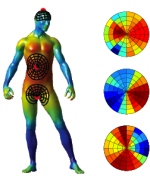
In this work, we present intrinsic shape context (ISC) descriptors for 3D shapes. We generalize to surfaces the polar sampling of the image domain used in shape contexts; for this purpose, we chart the surface by shooting geodesic outwards from the point being analyzed; ‘angle’ is treated as tantamount to geodesic shooting direction, and radius as geodesic distance. To deal with orientation ambiguity, we exploit properties of the Fourier transform. Our charting method is intrinsic, i.e., invariant to isometric shape transformations. The resulting descriptor is a meta-descriptor that can be applied to any photometric or geometric property field defined on the shape, in particular, we can leverage recent developments in intrinsic shape analysis and construct ISC based on state-of-the-art dense shape descriptors such as heat kernel signatures. Our experiments demonstrate a notable improvement in shape matching on standard benchmarks.
A game-theoretic approach to deformable shape matching
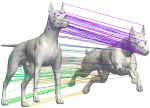
We consider the problem of minimum distortion intrinsic correspondence between deformable shapes, many useful formulations of which give rise to the NP-hard quadratic assignment problem (QAP). Previous attempts to use the spectral relaxation have had limited success due to the lack of sparsity of the obtained “fuzzy” solution. In this paper, we adopt the recently introduced alternative L1 relaxation of the QAP based on the principles of game theory. We relate it to the Gromov and Lipschitz metrics between metric spaces and demonstrate on state-of-the-art benchmarks that the proposed approach is capable of finding very accurate sparse correspondences between deformable shapes.
Eurographics Workshop on 3D Object Retrieval

This book contains the research work presented at fifth Eurographics Workshop on 3D Object Retrieval (3DOR) held in Cagliari, Italy on May 13, 2012. The 3DOR workshop series was started in Crete (2008), and then held in Munich (2009), Norrkoping (2010) and Llandudno (2011), always as a co-event of the Annual Conference of the European Association for Computer Graphics (Eurographics). All five such workshops are successful examples of international cooperation and the attendance demonstrates the relevance of focused topics. Demonstrating the increasing importance of the workshop, a record number of 23 papers were submitted this year. These papers were reviewed by an international Program Committee of 35 external experts in the area. Based on their recommendations, a selection of nine long papers was accepted for presentation at the workshop, giving an acceptance rate below 40%. Additionally, six poster presentations describing timely research results of high quality were included in the workshop program. Similarly to the previous editions of the 3DOR workshop, this year’s event hosted the seventh Shape Retrieval Contest (SHREC’12). The goal of the contest is to evaluate the effectiveness of 3D-shape retrieval algorithms, thus playing an important role in the evolution of 3D Object Retrieval research. SHREC’12 contributes to the proceedings with four additional papers that detail the results of the competition. We are grateful to the Eurographics association for their support, and to all reviewers for ensuring a high-quality program despite the tight schedule. Special thanks are also to Stefanie Behnke for her constant and timely attention. Finally, we hope that this workshop proves useful to all participants and sets the ground for long-term interaction, collaboration, and identification of future directions and potential problems in the field.
Stable volumetric features in deformable shapes

Region feature detectors and descriptors have become a successful and popular alternative to point descriptors in image analysis due to their high robustness and repeatability, leading to a significant interest in the shape analysis community in finding analogous approaches in the 3D world. Recent works have successfully extended the maximally stable extremal region (MSER) detection algorithm to surfaces. In many applications, however, a volumetric shape model is more appropriate, and modeling shape deformations as approximate isometries of the volume of an object, rather than its boundary, better captures natural behavior of non-rigid deformations. In this paper, we formulate a diffusion-geometric framework for volumetric stable component detection and description in deformable shapes. An evaluation of our method on the SHREC’11 feature detection benchmark and SCAPE human body scans shows its potential as a source of high-quality features. Examples demonstrating the drawbacks of surface stable components and the advantage of their volumetric counterparts are also presented.
Group-valued regularization for analysis of articulated motion

We present a novel method for estimation of articulated motion in depth scans. The method is based on a framework for regularization of vector- and matrix- valued functions on parametric surfaces. We extend augmented-Lagrangian total variation regularization to smooth rigid motion cues on the scanned 3D surface obtained from a range scanner. We demonstrate the resulting smoothed motion maps to be a powerful tool in articulated scene understanding, providing a basis for rigid parts segmentation, with little prior assumptions on the scene, despite the noisy depth measurements that often appear in commodity depth scanners.
Parallelized algorithms for rigid surface alignment on GPU
Alignment and registration of rigid surfaces is a fundamental computational geometric problem with applications ranging from medical imaging, automated target recognition, and robot navigation just to mention a few. The family of the iterative closest point (ICP) algorithms introduced by Chen and Medioni and Besl and McKey and improved over the three decades that followed constitute a classical to the problem. However, with the advent of geometry acquisition technologies and applications they enable, it has become necessary to align in real time dense surfaces containing millions of points. The classical ICP algorithms, being essentially sequential procedures, are unable to address the need. In this study, we follow the recent work by Mitra et al. considering ICP from the point of view of point-to-surface Euclidean distance map approximation. We propose a variant of a k-d tree data structure to store the approximation, and show its efficient parallelization on modern graphics processors. The flexibility of our implementation allows using different distance approximation schemes with controllable trade-off between accuracy and complexity. It also allows almost straightforward adaptation to richer transformation groups. Experimental evaluation of the proposed approaches on a state-of-the-art GPU on very large datasets containing around 106 vertices shows real-time performance superior by up to three orders of magnitude compared to an efficient CPU-based version.
Articulated motion segmentation of point clouds by group-valued regularization

Motion segmentation for articulated objects is an important topic of research. Yet such a segmentation should be as free as possible from underlying assumptions so as to fit general scenes and objects. In this paper we demonstrate an algorithm for articulated motion segmentation of 3D point clouds, free of any assumptions on the underlying model and yet firmly set in a well-defined variational framework. Results on scanned images show the generality of the proposed technique and its robustness to scanning artifacts and noise.
Affine-invariant photometric heat kernel signatures

In this paper, we explore the use of the diffusion geometry framework for the fusion of geometric and photometric information in local shape descriptors. Our construction is based on the definition of a modified metric, which combines geometric and photometric information, and then the diffusion process on the shape manifold is simulated. Experimental results show that such data fusion is useful in coping with shape retrieval experiments, where pure geometric and pure photometric methods fail. Apart from retrieval task the proposed diffusion process may be employed in other applications.
Stable semi-local features for non-rigid shapes
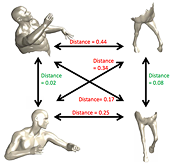
Feature-based analysis is becoming a very popular approach for geometric shape analysis. Following the success of this approach in image analysis, there is a growing interest in finding analogous methods in the 3D world. Maximally stable component detection is a low computation cost and high repeatability method for feature detection in images. In this study, a diffusion-geometry based framework for stable component detection is presented, which can be used for geometric feature detection in deformable shapes. The vast majority of studies of deformable 3D shapes models them as the two-dimensional boundary of the volume of the shape. Recent works have shown that a volumetric shape model is advantageous in numerous ways as it better captures the natural behavior of non-rigid deformations. We show that our framework easily adapts to this volumetric approach, and even demonstrates superior performance. A quantitative evaluation of our methods on the SHREC’10 and SHREC’11 feature detection benchmarks as well as qualitative tests on the SCAPE dataset show its potential as a source of high-quality features. Examples demonstrating the drawbacks of surface stable components and the advantage of their volumetric counterparts are also presented.
Group-valued regularization for motion segmentation of articulated shapes
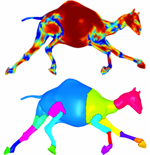
Motion-based segmentation is an important tool for the analysis of articulated shapes. As such, it plays an important role in mechanical engineering, computer graphics, and computer vision. In this chapter, we study motion-based segmentation of 3D articulated shapes. We formulate motion-based surface segmentation as a piecewise-smooth regularization problem for the transformations between several poses. Using Lie-group representation for the transformation at each surface point, we obtain a simple regularized fitting problem. An Ambrosio-Tortorelli scheme of a generalized Mumford-Shah model gives us the segmentation functional without assuming prior knowledge on the number of parts or even the articulated nature of the object. Experiments on several standard datasets compare the results of the proposed method to state-of-the-art algorithms.
3D features, surface descriptors, and object descriptors

The computer vision and pattern recognition communities have recently witnessed a surge of feature-based methods in numerous applications including object recognition and image retrieval. Similar concepts and analogous approaches are penetrating the world of 3D shape analysis, in a variety of areas including non-rigid shape retrieval and matching. In this chapter, we present the state-of-the-art of feature-based approaches in 3D shape analysis.
Spectral descriptors for deformable shapes

Informative and discriminative feature descriptors play a fundamental role in deformable shape analysis. For example, they have been successfully employed in correspondence, registration, and retrieval tasks. In the recent years, significant attention has been devoted to descriptors obtained from the spectral decomposition of the Laplace-Beltrami operator associated with the shape. Notable examples in this family are the heat kernel signature (HKS) and the wave kernel signature (WKS). Laplacian-based descriptors achieve state-of-the-art performance in numerous shape analysis tasks; they are computationally efficient, isometry-invariant by construction, and can gracefully cope with a variety of transformations. In this paper, we formulate a generic family of parametric spectral descriptors. We argue that in order to be optimal for a specific task, the descriptor should take into account the statistics of the corpus of shapes to which it is applied (the “signal”) and those of the class of transformations to which it is made insensitive (the “noise”). While such statistics are hard to model axiomatically, they can be learned from examples. Following the spirit of the Wiener filter in signal processing, we show a learning scheme for the construction of optimal spectral descriptors and relate it to Mahalanobis metric learning. The superiority of the proposed approach is demonstrated on the SHREC’10 benchmark.
Affine-invariant diffusion geometry for the analysis of deformable 3D shapes
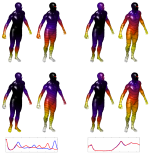
We introduce an (equi-)affine invariant diffusion geometry by which surfaces that go through squeeze and shear transformations can still be properly analyzed. The definition of an affine invariant metric enables us to construct an invariant Laplacian from which local and global geometric structures are extracted. Applications of the proposed framework demonstrate its power in generalizing and enriching the existing set of tools for shape analysis.
Shape recognition with spectral distances
Recent works have shown the use of diffusion geometry for various pattern recognition applications, including non-rigid shape analysis. In this paper, we introduce spectral shape distance as a general framework for distribution-based shape similarity and show that two recent methods for shape similarity due to Rustamov and Mahmoudi & Sapiro are particular cases thereof.
A correspondence-less approach to matching of deformable shapes
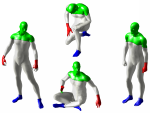
Finding a match between partially available deformable shapes is a challenging problem with numerous applications. The problem is usually approached by computing local descriptors on a pair of shapes and then establishing a point-wise correspondence between the two. In this paper, we introduce an alternative correspondence-less approach to matching fragments to an entire shape undergoing a non-rigid deformation. We use diffusion geometric descriptors and optimize over the integration domains on which the integral descriptors of the two parts match. The problem is regularized using the Mumford-Shah functional. We show an efficient discretization based on the Ambrosio-Tortorelli approximation generalized to triangular meshes. Experiments demonstrating the success of the proposed method are presented.
Photometric heat kernel signatures

In this paper, we explore the use of the diffusion geometry framework for the fusion of geometric and photometric information in local heat kernel signature shape descriptors. Our construction is based on the definition of a diffusion process on the shape manifold embedded into a high-dimensional space where the embedding coordinates represent the photometric information. Experimental results show that such data fusion is useful in coping with different challenges of shape analysis where pure geometric and pure photometric methods fail.
Deformable shape retrieval by learning diffusion kernels

In classical signal processing, it is common to analyze and process signals in the frequency domain, by representing the signal in the Fourier basis, and filtering it by applying a transfer function on the Fourier coefficients. In some applications, it is possible to design an optimal filter. A classical example is the Wiener filter that achieves a minimum mean squared error estimate for signal denoising. Here, we adopt similar concepts to construct optimal diffusion geometric shape descriptors. The analogy of Fourier basis are the eigenfunctions of the Laplace-Beltrami operator, in which many geometric constructions such as diffusion metrics, can be represented. By designing a filter of the Laplace-Beltrami eigenvalues, it is theoretically possible to achieve invariance to different shape transformations, like scaling. Given a set of shape classes with different transformations, we learn the optimal filter by minimizing the ratio between knowingly similar and knowingly dissimilar diffusion distances it induces. The output of the proposed framework is a filter that is optimally tuned to handle transformations that characterize the training set.
Group-valued regularization framework for motion segmentation of dynamic non-rigid shapes
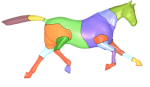
Understanding of articulated shape motion plays an important role in many applications in the mechanical engineering, movie industry, graphics, and vision communities. In this paper, we study motion-based segmentation of articulated 3D shapes into rigid parts. We pose the problem as finding a group-valued map between the shapes describing the motion, forcing it to favor piecewise rigid motions. Our computation follows the spirit of the Ambrosio-Tortorelli scheme for Mumford-Shah segmentation, with a diffusion component suited for the group nature of the motion model. Experimental results demonstrate the effectiveness of the proposed method in non-rigid motion segmentation.
Discrete minimum distortion correspondence problems for non-rigid shape matching
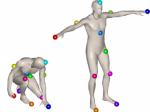
Similarity and correspondence are two fundamental archetype problems in shape analysis, encountered in numerous application in computer vision and pattern recognition. Many methods for shape similarity and correspondence boil down to the minimum-distortion correspondence problem, in which two shapes are endowed with certain structure, and one attempts to find the matching with smallest structure distortion between them. Defining structures invariant to some class of shape transformations results in an invariant minimum-distortion correspondence or similarity. In this paper, we model shapes using local and global structures, formulate the invariant correspondence problem as binary graph labeling, and show how different choice of structure results in invariance under various classes of deformations.
Shape palindromes: analysis of intrinsic symmetries in 2D articulated shapes
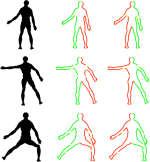
Analysis of intrinsic symmetries of non-rigid and articulated shapes is an important problem in pattern recognition with numerous applications ranging from medicine to computational aesthetics. Considering articulated planar shapes as closed curves, we show how to represent their extrinsic and intrinsic symmetries as self-similarities of local descriptor sequences, which in turn have simple interpretation in the frequency domain. The problem of symmetry detection and analysis thus boils down to analysis of descriptor sequence patterns. For that purpose, we show two efficient computational methods: one based on Fourier analysis, and another on dynamic programming. Metaphorically, the later can be compared to finding palindromes in text sequences.
Boosted metric learning for 3D multi-modal deformable registration
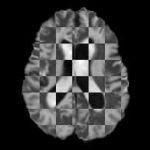
Defining a suitable metric is one of the biggest challenges in deformable image fusion from different modalities. In this paper, we propose a novel approach for multi-modal metric learning in the deformable registration framework that consists of embedding data from both modalities into a common metric space whose metric is used to parametrize the similarity. Specifically, we use image representation in the Fourier/Gabor space which introduces invariance to the local pose parameters, and the Hamming metric as the target embedding space, which allows constructing the embedding using boosted learning algorithms. The resulting metric is incorporated into a discrete optimization framework. Very promising results demonstrate the potential of the proposed method.
Affine-invariant geodesic geometry of deformable 3D shapes

Natural objects can be subject to various transformations yet still preserve properties that we refer to as invariants. Here, we use definitions of affine invariant arclength for surfaces in R3 in order to extend the set of existing non-rigid shape analysis tools. We show that by re-defining the surface metric as its equi-affine version, the surface with its modified metric tensor can be treated as a canonical Euclidean object on which most classical Euclidean processing and analysis tools can be applied. The new definition of a metric is used to extend the fast marching method technique for computing geodesic distances on surfaces, where now, the distances are defined with respect to an affine invariant arclength. Applications of the proposed framework demonstrate its invariance, efficiency, and accuracy in shape analysis.
Diffusion-geometric maximally stable component detection in deformable shapes
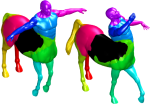
Maximally stable component detection is a very popular method for feature analysis in images, mainly due to its low computation cost and high repeatability. With the recent advance of feature-based methods in geometric shape analysis, there is significant interest in finding analogous approaches in the 3D world. In this paper, we formulate a diffusion-geometric framework for stable component detection in non-rigid 3D shapes, which can be used for geometric feature detection and description. A quantitative evaluation of our method on the SHREC’10 feature detection benchmark shows its potential as a source of high-quality features.
Shape Google: geometric words and expressions for invariant shape retrieval

The computer vision and pattern recognition communities have recently witnessed a surge of feature-based methods in object recognition and image retrieval applications. These methods allow representing images as collections of “visual words” and treat them using text search approaches following the “bag of features” paradigm. In this paper, we explore analogous approaches in the 3D world applied to the problem of non-rigid shape retrieval in large databases. Using multiscale diffusion heat kernels as “geometric words”, we construct compact and informative shape descriptors by means of the “bag of features” approach. We also show that considering pairs of geometric words (“geometric expressions”) allows creating spatially-sensitive bags of features with better discriminativity. Finally, adopting metric learning approaches, we show that shapes can be efficiently represented as binary codes. Our approach achieves state-of-the-art results on the SHREC 2010 large-scale shape retrieval benchmark.
Metric approaches to invariant shape similarity
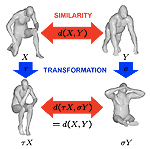
Non-rigid shapes are ubiquitous in Nature and are encountered at all levels of life, from macro to nano. The need to model such shapes and understand their behavior arises in many applications in imaging sciences, pattern recognition, computer vision, and computer graphics. Of particular importance is understanding which properties of the shape are attributed to deformations and which are invariant, i.e., remain unchanged. This chapter presents an approach to non- rigid shapes from the point of view of metric geometry. Modeling shapes as metric spaces, one can pose the problem of shape similarity as the similarity of metric spaces and harness tools from theoretical metric geometry for the computation of such a similarity.
Affine-invariant geodesic geometry of deformable 3D shapes

Natural objects can be subject to various transformations yet still preserve properties that we refer to as invariants. Here, we use definitions of affine invariant arclength for surfaces in R3 in order to extend the set of existing non-rigid shape analysis tools. In fact, we show that by re-defining the surface metric as its equi-affine version, the surface with its modified metric tensor can be treated as a canonical Euclidean object on which most classical Euclidean processing and analysis tools can be applied. The new definition of a metric is used to extend the fast marching method technique for computing geodesic distances on surfaces, where now, the distances are defined with respect to an affine invariant arclength. Applications of the proposed framework demonstrate its invariance, efficiency, and accuracy in shape analysis.
Affine-invariant diffusion geometry for the analysis of deformable 3D shapes

We introduce an (equi-)affine invariant diffusion geometry by which surfaces that go through squeeze and shear transformations can still be properly analyzed. The definition of an affine invariant metric enables us to construct an invariant Laplacian from which local and global geometric structures are extracted. Applications of the proposed framework demon- strate its power in generalizing and enriching the existing set of tools for shape analysis.
Full and partial symmetries of non-rigid shapes
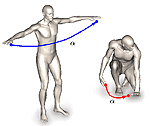
Symmetry and self-similarity is the cornerstone of Nature, exhibiting itself through the shapes of natural creations and ubiquitous laws of physics. Since many natural objects are symmetric, the absence of symmetry can often be an indication of some anomaly or abnormal behavior. Therefore, detection of asymmetries is important in numerous practical applications, including crystallography, medical imaging, and face recognition, to mention a few. Conversely, the assumption of underlying shape symmetry can facilitate solutions to many problems in shape reconstruction and analysis. Traditionally, symmetries are described as extrinsic geometric properties of the shape. While being adequate for rigid shapes, such a description is inappropriate for non-rigid ones: extrinsic symmetry can be broken as a result of shape deformations, while its intrinsic symmetry is preserved. In this paper, we present a generalization of symmetries for non-rigid shapes and a numerical framework for their analysis, addressing the problems of full and partial exact and approximate symmetry detection and classification.
A Gromov-Hausdorff framework with diffusion geometry for topologically-robust non-rigid shape matching
In this paper, the problem of non-rigid shape recognition is viewed from the perspective of metric geometry, and the applicability of diffusion distances within the Gromov-Hausdorff framework is explored. While the commonly used geodesic distance exploits the shortest path between points on the surface, the diffusion distance averages all paths connecting between the points. The diffusion distance provides an intrinsic distance measure which is robust, in particular to topological changes. Such changes may be a result of natural non-rigid deformations, as well as acquisition noise, in the form of holes or missing data, and representation noise due to inaccurate mesh construction. The presentation of the proposed framework is complemented with numerous examples demonstrating that in addition to the relatively low complexity involved in the computation of the diffusion distances between surface points, its recognition and matching performances favorably compare to the classical geodesic distances in the presence of topological changes between the non-rigid shapes.
Intrinsic regularity detection in 3D geometry

Automatic detection of symmetries, regularity, and repetitive structures in 3D geometry is a fundamental problem in shape analysis and pattern recognition with applications in computer vision and graphics. Especially challenging is to detect intrinsic regularity, where the repetitions are on an intrinsic grid, without any apparent Euclidean pattern to describe the shape, but rising out of (near) isometric deformation of the underlying surface. In this paper, we employ multidimensional scaling to reduce the problem of intrinsic structure detection to a simpler problem of 2D grid detection. Potential 2D grids are then identified using an autocorrelation analysis, refined using local fitting, validated, and finally projected back to the spatial domain. We test the detection algorithm on a variety of scanned plaster models in presence of imperfections like missing data, noise and outliers. We also present a range of applications including scan completion, shape editing, super-resolution, and structural correspondence.
Volumetric heat kernel signatures

Invariant shape descriptors are instrumental in numerous shape analysis tasks including deformable shape comparison, registration, classification, and retrieval. Most existing constructions model a 3D shape as a two-dimensional surface describing the shape boundary, typically represented as a triangular mesh or a point cloud. Using intrinsic properties of the surface, invariant descriptors can be designed. One such example is the recently introduced heat kernel signature, based on the Laplace-Beltrami operator of the surface. In many applications, however, a volumetric shape model is more natural and convenient. Moreover, modeling shape deformations as approximate isometries of the volume of an object, rather than its boundary, better captures natural behavior of non-rigid deformations in many cases. Here, we extend the idea of heat kernel signature to robust isometry-invariant volumetric descriptors, and show their utility in shape retrieval. The proposed approach achieves state-of-the-art results on the SHREC 2010 large-scale shape retrieval benchmark.
Diffusion symmetries of non-rigid shapes
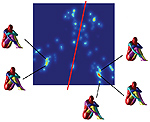
Detection and modeling of self-similarity and symmetry is important in shape recognition, matching, synthesis, and reconstruction. While the detection of rigid shape symmetries is well-established, the study of symmetries in non- rigid shapes is a much less researched problem. A particularly challenging setting is the detection of symmetries in non-rigid shapes affected by topological noise and asymmetric connectivity. In this paper, we treat shapes as metric spaces, with the metric induced by heat diffusion properties, and define non-rigid symmetries as self-isometries with respect to the diffusion metric. Experimental results show the advantage of the diffusion metric over the previously proposed geodesic metric for exploring intrinsic symmetries of bendable shapes with possible topological irregularities
SHREC 2010: robust large-scale shape retrieval benchmark
SHREC’10 robust large-scale shape retrieval benchmark simulates a retrieval scenario, in which the queries include multiple modifications and transformations of the same shape. The benchmark allows evaluating how algorithms cope with certain classes of transformations and what is the strength of the transformations that can be dealt with. The present paper is a report of the SHREC’10 robust large-scale shape retrieval benchmark results.
SHREC 2010: robust feature detection and description benchmark
Feature-based approaches have recently become very popular in computer vision and image analysis application, and are becoming a promising direction in shape retrieval applications. SHREC’10 robust feature detection and description benchmark simulates feature detection and description stage of feature-based shape retrieval algorithms. The benchmark tests the performance of shape feature detectors and descriptors under a wide variety of different transformations. The benchmark allows evaluating how algorithms cope with certain classes of transformations and what is the strength of the transformations that can be dealt with. The present paper is a report of the SHREC’10 robust feature detection and description benchmark results.
SHREC 2010: robust correspondence benchmark
SHREC’10 robust correspondence benchmark simulates a one-to-one shape matching scenario, in which one of the shapes undergoes multiple modifications and transformations. The benchmark allows evaluating how correspondence algorithms cope with certain classes of transformations and what is the strength of the transformations that can be dealt with. The present paper is a report of the SHREC’10 robust correspondence benchmark results.
ShapeGoogle: a computer vision approach for invariant shape retrieval

Feature-based methods have recently gained popularity in computer vision and pattern recognition communities, in applications such as object recognition and image retrieval. In this paper, we explore analogous approaches in the 3D world applied to the problem of non-rigid shape search and retrieval in large databases.
On reconstruction of non-rigid shapes with intrinsic regularization

Shape-from-X is a generic type of inverse problems in computer vision, in which a shape is reconstructed from some measurements. A specially challenging setting of this problem is the case in which the reconstructed shapes are non-rigid. In this paper, we propose a framework for intrinsic regularization of such problems. The assumption is that we have the geometric structure of a shape which is intrinsically (up to bending) similar to the one we would like to reconstruct. For that goal, we formulate a variation with respect to vertex coordinates of a triangulated mesh approximating the continuous shape. The numerical core of the proposed method is based on differentiating the fast marching update step for geodesic distance computation.
Topology-invariant similarity of nonrigid shapes
This paper explores the problem of similarity criteria between nonrigid shapes. Broadly speaking, such criteria are divided into intrinsic and extrinsic, the first referring to the metric structure of the object and the latter to how it is laid out in the Euclidean space. Both criteria have their advantages and disadvantages: extrinsic similarity is sensitive to nonrigid deformations, while intrinsic similarity is sensitive to topological noise. In this paper, we approach the problem from the perspective of metric geometry. We show that by unifying the extrinsic and intrinsic similarity criteria, it is possible to obtain a stronger topology-invariant similarity, suitable for comparing deformed shapes with different topology. We construct this new joint criterion as a tradeoff between the extrinsic and intrinsic similarity and use it as a set-valued distance. Numerical results demonstrate the efficiency of our approach in cases where using either extrinsic or intrinsic criteria alone would fail.
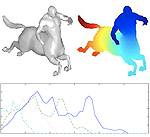
Partial similarity of objects, or how to compare a centaur to a horse
Similarity is one of the most important abstract concepts in human perception of the world. In computer vision, numerous applications deal with comparing objects observed in a scene with some a priori known patterns. Often, it happens that while two objects are not similar, they have large similar parts, that is, they are partially similar. Here, we present a novel approach to quantify partial similarity using the notion of Pareto optimality. We exemplify our approach on the problems of recognizing non-rigid geometric objects, images, and analyzing text sequences.
Partial similarity of shapes using a statistical significance measure

Partial matching of geometric structures is important in computer vision, pattern recognition and shape analysis applications. The problem consists of matching similar parts of shapes that may be dissimilar as a whole. Recently, it was proposed to consider partial similarity as a multi-criterion optimization problem trying to simultaneously maximize the similarity and the significance of the matching parts. A major challenge in that framework is providing a quantitative measure of the significance of a part of an object. Here, we define the significance of a part of a shape by its discriminative power with respect do a given shape database—that is, the uniqueness of the part. We define a point-wise significance density using a statistical weighting approach similar to the term frequency-inverse document frequency (tfidf) weighting employed in search engines. The significance measure of a given part is obtained by integrating over this density. Numerical experiments show that the proposed approach produces intuitive significant parts, and demonstrate an improvement in the performance of partial matching between shapes.
Parallel algorithms for approximation of distance maps on parametric surfaces
We present an efficient O(n) numerical algorithm for first-order approximation of geodesic distances on geometry images, where n is the number of points on the surface. The structure of our algorithm allows efficient implementation on parallel architectures. Two implementations on a SIMD processor and on a GPU are discussed. Numerical results demonstrate up to four orders of magnitude improvement in execution time compared to the state-of-the-art algorithms.
Regularized partial matching of rigid shapes
Matching of rigid shapes is an important problem in numerous applications across the boundary of computer vision, pattern recognition and computer graphics communities. A particularly challenging setting of this problem is partial matching, where the two shapes are dissimilar in general but have significant similar parts. In this paper, we show a rigorous approach allowing to find matching parts of rigid shapes with controllable size and regularity. The regularity term we use is similar to the spirit of the Mumford-Shah functional, extended to non-Euclidean spaces. Numerical experiments show that the regularized partial matching produces better results compared to the non-regularized one.
Analysis of two-dimensional non-rigid shapes
Analysis of deformable two-dimensional shapes is an important problem, encountered in numerous pattern recognition, computer vision, and computer graphics applications. In this paper, we address three major problems in the analysis of non-rigid shapes: similarity, partial similarity, and correspondence. We present an axiomatic construction of similarity criteria for deformation-invariant shape comparison, based on intrinsic geometric properties of the shapes, and show that such criteria are related to the Gromov-Hausdorff distance. Next, we extend the problem of similarity computation to shapes which have similar parts but are dissimilar when considered as a whole and present a construction of set-valued distances, based on the notion of Pareto optimality. Finally, we show that the correspondence between non-rigid shapes can be obtained as a byproduct of the non-rigid similarity problem. As a numerical framework, we use the generalized multidimensional scaling (GMDS) method, which is the numerical core of the three problems addressed in this paper.
Not only size matters: regularized partial matching of nonrigid shapes

Partial matching is probably one of the most challenging problems in nonrigid shape analysis. The problem consists of matching similar parts of shapes that are dissimilar on the whole and can assume different forms by undergoing nonrigid deformations. Conceptually, two shapes can be considered partially matching if they have significant similar parts, with the simplest definition of significance being the size of the parts. Thus, partial matching can be defined as a multcriterion optimization problem trying to simultaneously maximize the similarity and the size of these parts. In this paper, we propose a different definition of significance, taking into account the regularity of parts besides their size. The regularity term proposed here is similar to the spirit of the Mumford-Shah functional. Numerical experiments show that the regularized partial matching produces semantically better results compared to the non-regularized one.
Numerical geometry of non-rigid shapes

Deformable objects are ubiquitous in the world surrounding us, on all levels from micro to macro. The need to study such shapes and model their behavior arises in a wide spectrum of applications, ranging from medicine to security. In recent years, non-rigid shapes have attracted growing interest, which has led to rapid development of the field, where state-of-the-art results from very different sciences – theoretical and numerical geometry, optimization, linear algebra, graph theory, machine learning and computer graphics, to mention several – are applied to find solutions.
This book gives an overview of the current state of science in analysis and synthesis of non-rigid shapes. Everyday examples are used to explain concepts and to illustrate different techniques. The presentation unfolds systematically and numerous figures enrich the engaging exposition. Practice problems follow at the end of each chapter, with detailed solutions to selected problems in the appendix. A gallery of colored images enhances the text.
This book will be of interest to graduate students, researchers and professionals in different fields of mathematics, computer science and engineering. It may be used for courses in computer vision, numerical geometry and geometric modeling and computer graphics or for self-study.
Topologically constrained isometric embedding
We present a new algorithm for nonlinear dimensionality reduction that consistently uses global information, which enables understanding the intrinsic geometry of non-convex manifolds. Compared to methods that consider only local information, our method appears to be more robust to noise. We demonstrate the performance of our algorithm and compare it to state-of-the-art methods on synthetic as well as real data.
Embedded system for 3D shape reconstruction

Many applications that use three-dimensional scanning require a low cost, accurate and fast solution. This paper presents a fixed-point implementation of a real time active stereo threedimensional acquisition system on a Texas Instruments DM6446 EVM board which meets these requirements. A time-multiplexed structured light reconstruction technique is described and a fixed point algorithm for its implementation is proposed. This technique uses a standard camera and a standard projector. The fixed point reconstruction algorithm runs on the DSP core while the ARM controls the DSP and is responsible for communication with the camera and projector. The ARM uses the projector to project coded light and the camera to capture a series of images. The captured data is sent to the DSP. The DSP, in turn, performs the 3D reconstruction and returns the results to the ARM for storing. The inter-core communication is performed using the xDM interface and VISA API. Performance evaluation of a fully working prototype proves the feasibility of a fixed-point embedded implementation of a real time three-dimensional scanner, and the suitability of the DM6446 chip for such a system.
Calculus of non-rigid surfaces for geometry and texture manipulation

We present a geometric framework for automatically finding intrinsic correspondence between three-dimensional nonrigid objects. We model object deformation as near isometries and find the correspondence as the minimum-distortion mapping. A generalization of multidimensional scaling is used as the numerical core of our approach. As a result, we obtain the possibility to manipulate the extrinsic geometry and the texture of the objects as vectors in a linear space. We demonstrate our method on the problems of expression-invariant texture mapping onto an animated three-dimensional face, expression exaggeration, morphing between faces, and virtual body painting.
Rock, Paper, and Scissors: extrinsic vs. intrinsic similarity of non-rigid shapes

This paper explores similarity criteria between non-rigid shapes. Broadly speaking, such criteria are divided into intrinsic and extrinsic, the first referring to the metric structure of the objects and the latter to the geometry of the shapes in the Euclidean space. Both criteria have their advantages and disadvantages; extrinsic similarity is sensitive to non-rigid deformations of the shapes, while intrinsic similarity is sensitive to topological noise. Here, we present an approach unifying both criteria in a single distance. Numerical results demonstrate the robustness of our approach in cases where using only extrinsic or intrinsic criteria fail.
Weighted distance maps computation on parametric three-dimensional manifolds
We propose an effcient computational solver for the eikonal equations on parametric three-dimensional manifolds. Our approach is based on the fast marching method for solving the eikonal equation in O(n log n) steps by numerically simulating wavefront propagation. The obtuse angle splitting problem is reformulated as a set of small integer linear programs, that can be solved in O(n). Numerical simulations demonstrate the accuracy of the proposed algorithm.
Paretian similarity for partial comparison of non-rigid objects
In this paper, we address the problem of partial comparison of non-rigid objects. We introduce a new class of set-valued distances, related to the concept of Pareto optimality in economics. Such distances allow to capture intrinsic geometric similarity between parts of non-rigid objects, obtaining semantically meaningful comparison results. The numerical implementation of our method is computationally efficient and is similar to GMDS, a multidimensional scaling-like continuous optimization problem.
Partial similarity of objects and text sequences
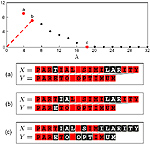
Similarity is one of the most important abstract concepts in the human perception of the world. In computer vision, numerous applications deal with comparing objects observed in a scene with some a priori known patterns. Often, it happens that while two objects are not similar, they have large similar parts, that is, they are partially similar. Here, we present a novel approach to quantify this semantic definition of partial similarity using the notion of Pareto optimality. We exemplify our approach on the problems of recognizing non-rigid objects and analyzing text sequences.
Expression-invariant representation of faces
We present an efficient computational framework for isometry-invariant comparison of smooth surfaces. We formulate the Gromov-Hausdorff distance as a multidimensional scaling (MDS)-like continuous optimization problem. In order to construct an efficient optimization scheme, we develop a numerical tool for interpolating geodesic distances on a sampled surface from precomputed geodesic distances between the samples. For isometry-invariant comparison of surfaces in the case of partially missing data, we present the partial embedding distance, which is computed using a similar scheme. The main idea is finding a minimum-distortion mapping from one surface to another while considering only relevant geodesic distances. We discuss numerical implementation issues and present experimental results that demonstrate its accuracy and efficiency.
Story of Cinderella: biometrics and isometry-invariant distances

In this chapter, we address the question of what are the facial measures one could use in order to distinguish between people. Our starting point is the fact that the expressions of our face can, in most cases, be modeled as isometries, which we validate empirically. Then, based on this observation, we introduce a technique that enables us to distinguish between people based on the intrinsic geometry of their faces. We provide empirical evidence that the proposed geometric measures are invariant to facial expressions and relate our findings to the broad context of biometric methods, ranging from modern face recognition technologies to fairy tales and biblical stories.
Symmetries of non-rigid shapes
Symmetry and self-similarity is the cornerstone of Nature, exhibiting itself through the shapes of natural creations and ubiquitous laws of physics. Since many natural objects are symmetric, the absence of symmetry can often be an indication of some anomaly or abnormal behavior. Therefore, detection of asymmetries is important in numerous practical applications, including crystallography, medical imaging, and face recognition, to mention a few. Conversely, the assumption of underlying shape symmetry can facilitate solutions to many problems in shape reconstruction and analysis. Traditionally, symmetries are described as extrinsic geometric properties of the shape. While being adequate for rigid shapes, such a description is inappropriate for non-rigid ones. Extrinsic symmetry can be broken as a result of shape deformations, while its intrinsic symmetry is preserved. In this paper, we pose the problem of finding intrinsic symmetries of non-rigid shapes and propose an efficient method for their computation.
Robust expression-invariant face recognition from partially missing data
Recent studies on three-dimensional face recognition proposed to model facial expressions as isometries of the facial surface. Based on this model, expression-invariant signatures of the face were constructed by means of approximate isometric embedding into flat spaces. Here, we apply a new method for measuring isometry-invariant similarity between faces by embedding one facial surface into another. We demonstrate that our approach has several significant advantages, one of which is the ability to handle partially missing data. Promising face recognition results are obtained in numerical experiments even when the facial surfaces are severely occluded.
Matching two-dimensional articulated shapes using generalized multidimensional scaling
We present a theoretical and computational framework for matching of two-dimensional articulated shapes. Assuming that articulations can be modeled as near-isometries, we show an axiomatic construction of an articulation-invariant distance between shapes, formulated as a generalized multidimensional scaling (GMDS) problem and solved efficiently. Some numerical results demonstrating the accuracy of our method are presented.
Face2Face: an isometric model for facial animation
A geometric framework for finding intrinsic correspondence between animated 3D faces is presented. We model facial expressions as isometries of the facial surface and find the correspondence between two faces as the minimum-distortion mapping. Generalized multidimensional scaling is used for this goal. We apply our approach to texture mapping onto 3D video, expression exaggeration and morphing between faces.
Multigrid multidimensional scaling
Multidimensional scaling (MDS) is a generic name for a family of algorithms that construct a configuration of points in a target metric space from information about inter-point distances measured in some other metric space. Large-scale MDS problems often occur in data analysis, representation, and visualization. Solving such problems efficiently is of key importance in many applications. In this paper, we present a multigrid framework for MDS problems. We demonstrate the performance of our algorithm on dimensionality reduction and isometric embedding problems, two classical problems requiring efficient large-scale MDS. Simulation results show that the proposed approach significantly outperforms conventional MDS algorithms.
Generalized multidimensional scaling: a framework for isometry-invariant partial surface matching

An efficient algorithm for isometry-invariant matching of surfaces is presented. The key idea is computing the minimum-distortion mapping between two surfaces. For this purpose, we introduce the generalized multidimensional scaling, a computationally efficient continuous optimization algorithm for finding the least distortion embedding of one surface into another. The generalized multidimensional scaling algorithm allows for both full and partial surface matching. As an example, it is applied to the problem of expression- invariant three-dimensional face recognition.
Expression invariant face recognition: faces as isometric surfaces

One of the hardest problems in face recognition is dealing with facial expressions. Finding an expression-invariant representation of the face could be a remedy for this problem. We suggest treating faces as deformable surfaces in the context of Riemannian geometry, and propose to approximate facial expressions as isometries of the facial surface. This way, we can define geometric invariants of a given face under different expressions. One such invariant is constructed by isometrically embedding the facial surface structure into a low-dimensional flat space. Based on this approach, we built an accurate three-dimensional face recognition system that is able to distinguish between identical twins under various facial expressions. In this chapter we show how under the near-isometric model assumption, the difficult problem of face recognition in the presence of facial expressions can be solved in a relatively simple way.
Three-dimensional face recognition

An expression-invariant 3D face recognition approach is presented. Our basic assumption is that facial expressions can be modeled as isometries of the facial surface. This allows to construct expression-invariant representations of faces using the canonical forms approach. The result is an efficient and accurate face recognition algorithm, robust to facial expressions that can distinguish between identical twins (the first two authors). We demonstrate a prototype system based on the proposed algorithm and compare its performance to classical face recognition methods. The numerical methods employed by our approach do not require the facial surface explicitly. The surface gradients field, or the surface metric, are sufficient for constructing the expression-invariant representation of any given face. It allows us to perform the 3D face recognition task while avoiding the surface reconstruction stage.
Expression-invariant face recognition via spherical embedding
Recently, it was proven empirically that facial expressions can be modeled as isometries, that is, geodesic distances on the facial surface were shown to be significantly less sensitive to facial expressions compared to Euclidean ones. Based on this assumption, the 3DFACE face recognition system was built. The system efficiently computes expression invariant signatures based on an isometry-invariant representation of the facial surface. One of the crucial steps in the recognition system was embedding of the face geometric structure into a Euclidean (flat) space. Here, we propose to replace the flat embedding by a spherical one to construct isometric invariant representations of the facial image. We refer to these new invariants as spherical canonical images. Compared to its Euclidean counterpart, spherical embedding leads to notably smaller metric distortion. We demonstrate experimentally that representations with lower embedding error lead to better recognition. In order to efficiently compute the invariants, we introduce a dissimilarity measure between the spherical canonical images based on the spherical harmonic transform.
Isometric embedding of facial surfaces into S^3

The problem of isometry-invariant representation and comparison of surfaces is of cardinal importance in pattern recognition applications dealing with deformable objects. Particularly, in three-dimensional face recognition treating facial expressions as isometries of the facial surface allows to perform robust recognition insensitive to expressions. Isometry-invariant representation of surfaces can be constructed by isometrically embedding them into some convenient space, and carrying out the comparison in that space. Presented here is a discussion on isometric embedding into S3, which appears to be superior over the previously used Euclidean space in sense of the representation accuracy.
Fusion of 2D and 3D data in three-dimensional face recognition

We discuss the synthesis between the 3D and the 2D data in three-dimensional face recognition. We show how to compensate for the illumination and facial expressions using the 3D facial geometry and present the approach of canonical images, which allows to incorporate geometric information into standard face recognition approaches.
Face recognition from facial surface metric

Recently, a 3D face recognition approach based on geometric invariant signatures, has been proposed. The key idea is a representation of the facial surface, invariant to isometric deformations, such as those resulting from facial expressions. One important stage in the construction of the geometric invariants involves in measuring geodesic distances on triangulated surfaces, which is carried out by the fast marching on triangulated domains algorithm. Proposed here is a method that uses only the metric tensor of the surface for geodesic distance computation. That is, the explicit integration of the surface in 3D from its gradients is not needed for the recognition task. It enables the use of simple and cost-efficient 3D acquisition techniques such as photometric stereo. Avoiding the explicit surface reconstruction stage saves computational time and reduces numerical errors.
Expression-invariant 3D face recognition

We present a novel 3D face recognition approach based on geometric invariants introduced by Elad and Kimmel. The key idea of the proposed algorithm is a representation of the facial surface, invariant to isometric deformations, such as those resulting from different expressions and postures of the face. The obtained geometric invariants allow mapping 2D facial texture images into special images that incorporate the 3D geometry of the face. These signature images are then decomposed into their principal components. The result is an efficient and accurate face recognition algorithm that is robust to facial expressions. We demonstrate the results of our method and compare it to existing 2D and 3D face recognition algorithms.